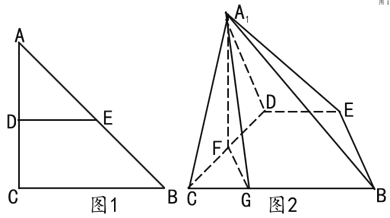
题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
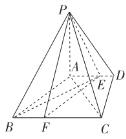
(1)点![]() 在
在![]() 上,
上,![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先证明四边形![]() 为平行四边形,得
为平行四边形,得![]() ,则
,则![]() ,又可得
,又可得![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)根据线面角定义找出![]() 与平面
与平面![]() 所成角,得
所成角,得![]() 的长度,然后建立空间直角坐标系,分别求出平面
的长度,然后建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的法向量,再利用向量法求出二面角
的法向量,再利用向量法求出二面角![]() 的余弦值.
的余弦值.
(1)∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴四边形![]() 是平行四边形,则
是平行四边形,则![]() ,∴
,∴![]() ,
,
∵![]() 底面
底面![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
则![]() ,即
,即![]() ,
,
取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则
,则![]() ,以
,以![]() 点为坐标原点建立如图所示的空间直角坐标系
点为坐标原点建立如图所示的空间直角坐标系![]() ,
,
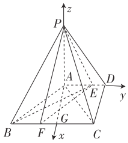
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则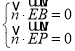 ,
,
即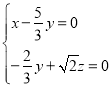 ,令
,令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是平面
是平面![]() 的一个法向量,∴
的一个法向量,∴![]() ,
,
即平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

【题目】对于很多人来说,提前消费的认识首先是源于信用卡,在那个工资不高的年代,信用卡绝对是神器,稍微大件的东西都是可以选择用信用卡来买,甚至于分期买,然后慢慢还!现在银行贷款也是很风靡的,从房贷到车贷到一般的现金贷.信用卡“忽如一夜春风来”,遍布了各大小城市的大街小巷.为了解信用卡在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下![]() 列联表(单位:人)
列联表(单位:人)
经常使用信用卡 | 偶尔或不用信用卡 | 合计 | |
40岁及以下 | 15 | 35 | 50 |
40岁以上 | 20 | 30 | 50 |
合计 | 35 | 65 | 100 |
(1)根据以上数据,能否在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关?
市使用信用卡情况与年龄有关?
(2)①现从所抽取的40岁及以下的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出4人赠送积分,求选出的4人中至少有3人偶尔或不用信用卡的概率;
②将频率视为概率,从![]() 市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为
市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
参考公式: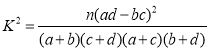 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】北京地铁八通线西起四惠站,东至土桥站,全长18.964km,共设13座车站.目前八通线执行2014年12月28日制订的计价标准,各站间计程票价(单位:元)如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | p>5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | /p> | 3 | 3 | ||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
(Ⅰ)在13座车站中任选两个不同的车站,求两站间票价不足5元的概率;
(Ⅱ)甲乙二人从四惠站上车乘坐八通线,各自任选另一站下车(二人可同站下车),记甲乙二人乘车购票花费之和为X元,求X的分布列;
(Ⅲ)若甲乙二人只乘坐八通线,甲从四惠站上车,任选另一站下车,记票价为![]() 元;乙从土桥站上车,任选另一站下车,记票价为
元;乙从土桥站上车,任选另一站下车,记票价为![]() 元.试比较
元.试比较![]() 和
和![]() 的方差
的方差![]() 和
和![]() 大小.(结论不需要证明)
大小.(结论不需要证明)