题目内容
【题目】对于很多人来说,提前消费的认识首先是源于信用卡,在那个工资不高的年代,信用卡绝对是神器,稍微大件的东西都是可以选择用信用卡来买,甚至于分期买,然后慢慢还!现在银行贷款也是很风靡的,从房贷到车贷到一般的现金贷.信用卡“忽如一夜春风来”,遍布了各大小城市的大街小巷.为了解信用卡在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了100人进行抽样分析,得到如下![]() 列联表(单位:人)
列联表(单位:人)
经常使用信用卡 | 偶尔或不用信用卡 | 合计 | |
40岁及以下 | 15 | 35 | 50 |
40岁以上 | 20 | 30 | 50 |
合计 | 35 | 65 | 100 |
(1)根据以上数据,能否在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关?
市使用信用卡情况与年龄有关?
(2)①现从所抽取的40岁及以下的网民中,按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人,然后,再从这10人中随机选出4人赠送积分,求选出的4人中至少有3人偶尔或不用信用卡的概率;
②将频率视为概率,从![]() 市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为
市所有参与调查的40岁以上的网民中随机抽取3人赠送礼品,记其中经常使用信用卡的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
参考公式: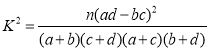 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)不能在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关;(2)①
市使用信用卡情况与年龄有关;(2)①![]() ;②分布列见解析,
;②分布列见解析,![]() ,
,![]()
【解析】
(1)计算![]() 再对照表格分析即可.
再对照表格分析即可.
(2)①根据分层抽样的方法可得经常使用信用卡的有![]() 人,偶尔或不用信用卡的有
人,偶尔或不用信用卡的有![]() 人,再根据超几何分布的方法计算3人或4人偶尔或不用信用卡的概率即可.
人,再根据超几何分布的方法计算3人或4人偶尔或不用信用卡的概率即可.
②利用二项分布的特点求解变量![]() 的分布列、数学期望和方差即可.
的分布列、数学期望和方差即可.
(1)由列联表可知,![]() ,因为
,因为![]() ,
,
所以不能在犯错误的概率不超过0.10的前提下认为![]() 市使用信用卡情况与年龄有关.
市使用信用卡情况与年龄有关.
(2)①依题意,可知所抽取的10名40岁及以下网民中,经常使用信用卡的有![]() (人),偶尔或不用信用卡的有
(人),偶尔或不用信用卡的有![]() (人).
(人).
则选出的4人中至少有3人偶尔或不用信用卡的概率![]() .
.
②由![]() 列联表,可知40岁以上的网民中,抽到经常使用信用卡的频率为
列联表,可知40岁以上的网民中,抽到经常使用信用卡的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,恰好抽到经常使用信用卡的市民的概率为
市市民中任意抽取1人,恰好抽到经常使用信用卡的市民的概率为![]() .
.
由题意得![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
故随机变量![]() 的数学期望为
的数学期望为![]() ,方差为
,方差为![]() .
.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
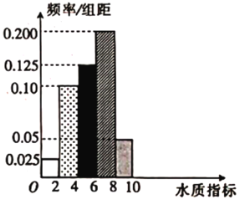
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】新《水污染防治法》已由中华人民共和国第十二届全国人民代表大会常务委员会第二十八次会议于2017年6月27日通过,自2018年1月1日起施行.2018年3月1日,某县某质检部门随机抽取了县域内100眼水井,检测其水质总体指标.
罗斯水质指数 | 02 | 24 | 46 | 68 | 810 |
水质状况 | 腐败污水 | 严重污染 | 污染 | 轻度污染 | 纯净 |
(1)求所抽取的100眼水井水质总体指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(2)①由直方图可以认为,100眼水井水质总体指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在(5.21,5.99)内的概率;
落在(5.21,5.99)内的概率;
②将频率视为概率,若某乡镇抽查5眼水井的水质,记这5眼水井水质总体指标值位于(6,10)内的井数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100眼水井总体指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.