题目内容
如图,正方形BCDE的边长为a,已知AB= BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:

(1)AB与DE所成角的正切值是 .
.
(2)三棱锥B-ACE的体积是 a3.
a3.
(3)AB∥CD.
(4)平面EAB⊥平面ADE.
其中正确的叙述有 (写出所有正确结论的编号).
 BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
BC,将直角△ABE沿BE边折起,A点在平面BCDE上的射影为D点,则对翻折后的几何体有如下描述:
(1)AB与DE所成角的正切值是
 .
.(2)三棱锥B-ACE的体积是
 a3.
a3.(3)AB∥CD.
(4)平面EAB⊥平面ADE.
其中正确的叙述有 (写出所有正确结论的编号).
(1)(2)(4)
翻折后得到的直观图如图所示.

AB与DE所成的角也就是AB与BC所成的角,即为∠ABC.
因为AD⊥平面BCDE,所以平面ADC⊥平面BCDE.
又因为四边形BCDE为正方形,
所以BC⊥CD.
可得BC⊥平面ACD.所以BC⊥AC.
因为BC=a,AB= BC=
BC= a,
a,
则AC= =
= a.
a.
在Rt△ABC中,tan∠ABC= =
= .故(1)正确;
.故(1)正确;
由AD= =a,可得
=a,可得
VB-ACE=VA-BCE= ×
× a2·a=
a2·a= ,故(2)正确;
,故(2)正确;
因为AB与CD异面,故(3)错;
因为AD⊥平面BCDE,所以平面ADE⊥平面BCDE.
又BE⊥ED,所以BE⊥平面ADE,故平面EAB⊥平面ADE,故(4)正确.

AB与DE所成的角也就是AB与BC所成的角,即为∠ABC.
因为AD⊥平面BCDE,所以平面ADC⊥平面BCDE.
又因为四边形BCDE为正方形,
所以BC⊥CD.
可得BC⊥平面ACD.所以BC⊥AC.
因为BC=a,AB=
 BC=
BC= a,
a,则AC=
 =
= a.
a.在Rt△ABC中,tan∠ABC=
 =
= .故(1)正确;
.故(1)正确;由AD=
 =a,可得
=a,可得VB-ACE=VA-BCE=
 ×
× a2·a=
a2·a= ,故(2)正确;
,故(2)正确;因为AB与CD异面,故(3)错;
因为AD⊥平面BCDE,所以平面ADE⊥平面BCDE.
又BE⊥ED,所以BE⊥平面ADE,故平面EAB⊥平面ADE,故(4)正确.

练习册系列答案
相关题目
 的圆锥
的圆锥 中,已知
中,已知 的直径
的直径 ,
, 是
是 的中点,
的中点, 是弦
是弦 的中点.
的中点.
 的平面角,并求出它的大小;
的平面角,并求出它的大小; 与
与 所成的角的正切值.
所成的角的正切值.





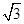 ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.



 πcm3
πcm3 πcm3
πcm3 πcm3
πcm3
 的三视图如图,则四棱锥
的三视图如图,则四棱锥

