题目内容

9．函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{3}）^{x}，x＜1}\\{lnx，x≥1}\end{array}\right.$，则方程f（f（a））=1解的个数为（　　）
A．1B．2C．3D．4

分析 利用换元法设f（a）=t，则方程等价为f（t）=1，根据指数函数和对数函数图象和性质求出t的值，利用数形结合进行求解即可．

解答 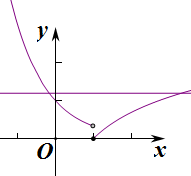解：令f（a）=t，则方程f[f（a）]=1等价为f（t）=1，
当t＜1时，由$（\frac{1}{3}）^{t}=1$，解得t=0，
当t≥1时，由lnt=1，解得t=e，
即f（a）=0，或f（a）=e，
作出函数f（x）的图象如图：
由图象可知方程f（a）=0的根只有一个，
方程f（a）=e的根有2个，
故方程f（f（a））=1解的个数为3个，
故选：C．

点评 本题主要考查函数方程根的个数的应用，利用换元法求出t的值是解决本题的关键．注意利用指数函数和对数函数的图象，结合数形结合是解决本题的关键．综合性较强．

练习册系列答案
相关题目
19．设函数f（x）=|x-$\frac{1}{a}$|+|x+a|≥m．则m的最大值是2．
20．已知函数$f（x）=2sin（{ωx-\frac{π}{6}}）+1（{x∈R}）$的图象的一条对称轴为x=π，其中ω为常数，且ω∈（1，2），则函数f（x）的最小正周期为（　　）
A．$\frac{3π}{5}$B．$\frac{6π}{5}$C．$\frac{9π}{5}$D．$\frac{12π}{5}$
17．设a=log2$\frac{1}{3}$，b=${e}^{-\frac{1}{2}}$，c=lnπ，则（　　）
A．c＜a＜bB．a＜c＜bC．a＜b＜cD．b＜a＜c
4．一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共n（n=13k，k∈N+）只，现在盒子上开一小孔，每次只能一只昆虫飞出（任意一只昆虫等可能地飞出），已知有2只昆虫先后飞出时，飞出的至少有1只是蜜蜂的概率是$\frac{25}{39}$．
（Ⅰ）若盒子中共有13只昆虫：
①求蜜蜂有几只；
②从盒子先后任意飞出3只昆虫，记飞出蜜蜂的只数为X，求随机变量X的分布列与期望E（X）；
（Ⅱ）若只有1只昆虫飞出时，飞出的是蝴蝶的概率是$\frac{5}{13}$．证明：从盒子先后任意飞出2只昆虫，至少有1只蝴蝶飞出的概率不大于$\frac{25}{39}$，并指出盒子中哪种昆虫的只数最少．
14．PM2.5是悬浮在空气中的直径小于或等于2.5微米的颗粒物，也成为入肺颗粒物，根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上的空气质量为超标．甲、乙两景区3月2日～3月21日20天内的PM2.5日均值如茎叶图所示：
（Ⅰ）将20天的PM2.5日均值分为五组[0，10），[10，20），[20，30），[30，40），[40，50]试作甲的频率分布直方图，并计算乙景区20天日均值的平均值；
（Ⅱ）已知甲、乙两景区3月6日～9日的PM2.5日均值依次为8、10、15、27；10、13、8、14，某游客欲在相邻的两天分游览甲、乙景区各一天，试求这两天的日均值的差小于5的概率．
1．在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
（Ⅰ）对任意a∈R，a*0=a；
（Ⅱ）对任意Ra，b∈R，a*b=ab+（a*0）+（b*0）．
关于函数f（x）=（ex）*$\frac{1}{{e}^{x}}$的性质，有如下说法：①函数f（x）的最小值为3；②函数f（x）为偶函数；③函数f（x）的单调递增区间为（-∞，0]．其中所有正确说法的序号为①②．
18．下列四个结论：其中正确结论的个数是（　　）
①命题“?x∈R，x-lnx＞0”的否定是“?x0∈R，x0-lnx0≤0”；
②命题“若x-sinx=0，则x=0”的逆否命题为“若x≠0，则x-sinx≠0”；
③“命题p∨q为真”是“命题p∧q为真”的充分不必要条件；
④若x＞0，则x＞sinx恒成立．
A．1个B．2个C．3个D．4个
17．设集合 A={y|y=lnx，x＞1}，集合B=$\left\{{x\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$，则A∩∁RB=（2，+∞）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网