题目内容
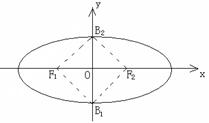
(本小题满分13分)已知椭圆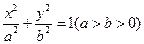 的两焦点
的两焦点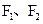 和短轴的两端点
和短轴的两端点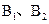 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为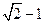 .
.
(1)求椭圆的标准方程;
(2)设P是椭圆上任一点,AB 是圆C:
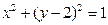 的任一条直径,求
的任一条直径,求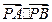 的
的
最大值.
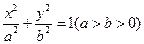 的两焦点
的两焦点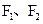 和短轴的两端点
和短轴的两端点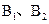 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为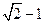 .
.
(1)求椭圆的标准方程;
(2)设P是椭圆上任一点,AB 是圆C:
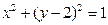 的任一条直径,求
的任一条直径,求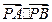 的
的最大值.
(1)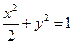 ;(2)8
;(2)8
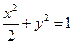 ;(2)8
;(2)8(1)由题意知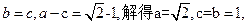
故椭圆的标准方程为
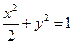 。………………………………………(5分)
。………………………………………(5分)
(2)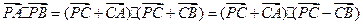 =
=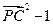
从而只需求出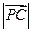 的最大值 ……………………………………………(9分)
的最大值 ……………………………………………(9分)
设P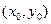 ,则有
,则有 ,即有
,即有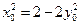 ,
,
又C(0,2),所以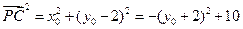 ,
,
而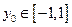 ,所以
,所以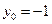 时,
时,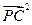 最大值为9,
最大值为9,
故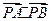 的最大值为8. ………………………………………………(13分)
的最大值为8. ………………………………………………(13分)
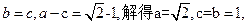
故椭圆的标准方程为

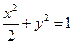 。………………………………………(5分)
。………………………………………(5分)(2)
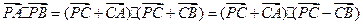 =
=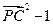
从而只需求出
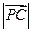 的最大值 ……………………………………………(9分)
的最大值 ……………………………………………(9分)设P
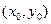 ,则有
,则有 ,即有
,即有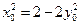 ,
,又C(0,2),所以
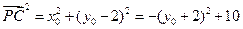 ,
,而
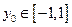 ,所以
,所以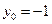 时,
时,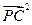 最大值为9,
最大值为9,故
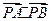 的最大值为8. ………………………………………………(13分)
的最大值为8. ………………………………………………(13分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为圆上一动点,点
为圆上一动点,点 在
在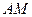 上,点
上,点 在
在 上,且满足
上,且满足 的轨迹为曲线
的轨迹为曲线 .
. 与(1)中所求点
与(1)中所求点 是坐
是坐 ,求△
,求△ 的面积的取值范围.
的面积的取值范围. c,0)三点,其中c>0.
c,0)三点,其中c>0.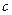 的式子表示);
的式子表示);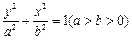 (其中
(其中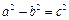 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,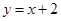 与抛物线
与抛物线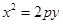 相交于A、B两点,O为原点,若
相交于A、B两点,O为原点,若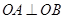 ,
,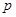 = ( )
= ( )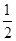 B.1 C.2 D.4
B.1 C.2 D.4 圆C:
圆C: 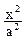 +
+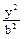 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=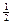 ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3).




 的焦距为( )
的焦距为( )



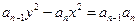 (
(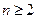 ,
,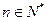 )的焦点在
)的焦点在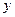 轴上,一条渐近线方程是
轴上,一条渐近线方程是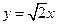 ,其中数列
,其中数列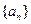 是以4为首项的正项数列,则数列
是以4为首项的正项数列,则数列



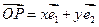 (其中
(其中 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若 =120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是
=120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是 
 ( )
( )


