题目内容
(本小题满分15分)平面直角坐标系xOy中,已知⊙M经过点F1(0,-c),F2(0,c),A( c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求⊙M的标准方程(用含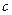 的式子表示);
的式子表示);
(2)已知椭圆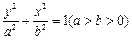 (其中
(其中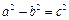 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,
⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
 c,0)三点,其中c>0.
c,0)三点,其中c>0.(1)求⊙M的标准方程(用含
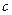 的式子表示);
的式子表示);(2)已知椭圆
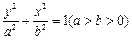 (其中
(其中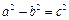 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
(1)⊙M的方程为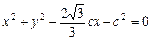 ,(2)①椭圆离心率的取值范围为
,(2)①椭圆离心率的取值范围为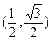 .②直线MF1与直线DF2的交点Q在定直线
.②直线MF1与直线DF2的交点Q在定直线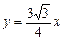 上
上
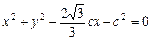 ,(2)①椭圆离心率的取值范围为
,(2)①椭圆离心率的取值范围为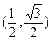 .②直线MF1与直线DF2的交点Q在定直线
.②直线MF1与直线DF2的交点Q在定直线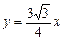 上
上(1)设⊙M的方程为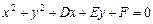 ,则由题设,得
,则由题设,得
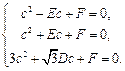 解得
解得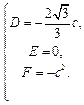 ⊙M的方程为
⊙M的方程为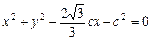 ,
,
⊙M的标准方程为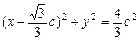 .
.
(2)①⊙M与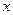 轴的两个交点
轴的两个交点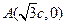 ,
,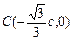 ,又
,又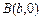 ,
,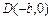 ,
,
由题设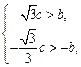 即
即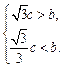 所以
所以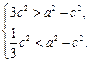 ………………………7分
………………………7分
解得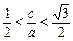 ,即
,即 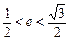 .
.
所以椭圆离心率的取值范围为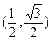 .……………10分
.……………10分
②由(1),得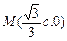 .由题设,得
.由题设,得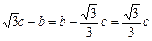 . ∴
. ∴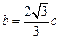 ,
,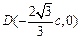 .
.
∴直线MF1的方程为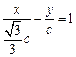 , ①
, ①
直线DF2的方程为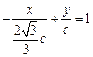 . ②
. ②
由①②,得直线MF1与直线DF2的交点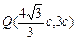 ,易知
,易知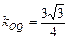 为定值,
为定值,
∴直线MF1与直线DF2的交点Q在定直线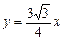 上.…………………15分
上.…………………15分
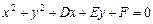 ,则由题设,得
,则由题设,得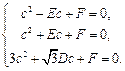 解得
解得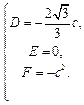 ⊙M的方程为
⊙M的方程为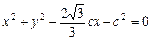 ,
,⊙M的标准方程为
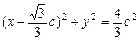 .
.(2)①⊙M与
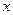 轴的两个交点
轴的两个交点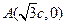 ,
,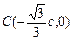 ,又
,又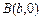 ,
,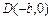 ,
,由题设
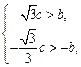 即
即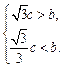 所以
所以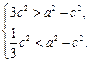 ………………………7分
………………………7分解得
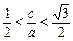 ,即
,即 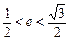 .
.所以椭圆离心率的取值范围为
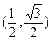 .……………10分
.……………10分②由(1),得
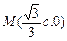 .由题设,得
.由题设,得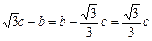 . ∴
. ∴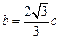 ,
,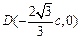 .
.∴直线MF1的方程为
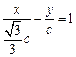 , ①
, ① 直线DF2的方程为
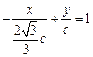 . ②
. ②由①②,得直线MF1与直线DF2的交点
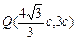 ,易知
,易知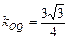 为定值,
为定值,∴直线MF1与直线DF2的交点Q在定直线
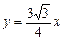 上.…………………15分
上.…………………15分
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的上顶点为
的上顶点为 ,椭圆
,椭圆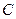 上两点
上两点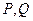 在
在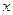 轴上的射影分别为左焦点
轴上的射影分别为左焦点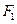 和右焦点
和右焦点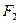 ,直线
,直线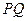 的斜率为
的斜率为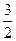 ,过点
,过点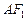 垂直的直线与
垂直的直线与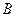 ,
,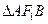 的外接圆为圆
的外接圆为圆 .
.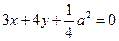 与圆
与圆 两点,且
两点,且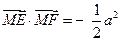 ,求椭圆方程;
,求椭圆方程;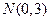 在椭圆C内部,若椭圆C上的点到点N的最远距离不大于
在椭圆C内部,若椭圆C上的点到点N的最远距离不大于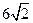 ,求椭圆C的短轴长的取值范围.
,求椭圆C的短轴长的取值范围.
 满足条件
满足条件 的点
的点 的轨迹是曲线
的轨迹是曲线 ,直线
,直线 与曲线
与曲线 两点
两点 如果
如果 且曲线
且曲线 ,使
,使 求
求
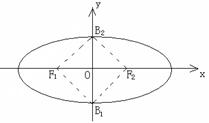
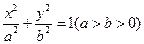 的两焦点
的两焦点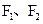 和短轴的两端点
和短轴的两端点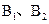 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为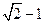 .
.
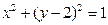 的任一条直径,求
的任一条直径,求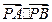 的
的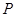 是抛物线
是抛物线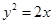 上的一个动点,则点
上的一个动点,则点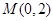 的距离与点
的距离与点


 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数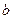 的取值;
的取值;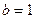 ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。 的长轴,若把该长轴2010等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
的长轴,若把该长轴2010等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点 ,设左焦点为
,设左焦点为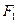 ,则
,则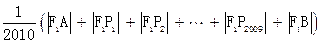 =
= 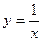 上一点A(1,1),则该曲线
上一点A(1,1),则该曲线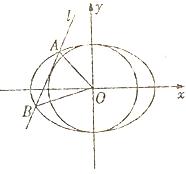
 :
: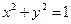 ,直线
,直线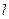 :
: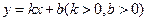 是圆的一条切线,且
是圆的一条切线,且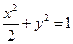 交于不同的两点
交于不同的两点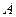 ,
,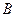 .
.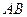 的长为
的长为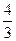 ,求直线
,求直线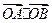 的值.
的值.