题目内容
8.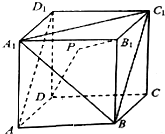 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{3}$] | C. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
分析 取BC1的中点E,作点B1在平面A1BC1内的投影O,过O作OF∥BC1交A1B于点F,连结B1D、A1E,以O为坐标原点,分别以OF、OE、OB1所在直线为x、y、z轴建立空间直角坐标系,利用cos<$\overrightarrow{P{B}_{1}}$,$\overrightarrow{B{C}_{1}}$>=$\frac{\overrightarrow{P{B}_{1}}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{P{B}_{1}}||\overrightarrow{B{C}_{1}}|}$计算即可.
解答 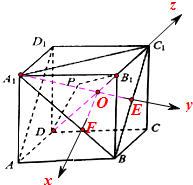 解:取BC1的中点E,作点B1在平面A1BC1内的投影O,
解:取BC1的中点E,作点B1在平面A1BC1内的投影O,
过O作OF∥BC1交A1B于点F,连结B1D、A1E,
以O为坐标原点,分别以OF、OE、OB1所在直线为x、y、z轴建立空间直角坐标系如图,
根据题意,易得D(0,0,-2$\sqrt{3}$),B1(0,0,$\sqrt{3}$),B($\frac{3}{2}$$\sqrt{2}$,$\frac{\sqrt{6}}{2}$,0),C1(-$\frac{3}{2}$$\sqrt{2}$,$\frac{\sqrt{6}}{2}$,0),
设P(x,y,0),则$\overrightarrow{PD}$=(-x,-y,-2$\sqrt{3}$),$\overrightarrow{P{B}_{1}}$=(-x,-y,$\sqrt{3}$),$\overrightarrow{B{C}_{1}}$=(-3$\sqrt{2}$,0,0),
∵|PD|+|PB1|=2+$\sqrt{13}$,
∴$\sqrt{{x}^{2}+{y}^{2}+12}$+$\sqrt{{x}^{2}+{y}^{2}+3}$=2+$\sqrt{13}$,
∴|$\overrightarrow{P{B}_{1}}$|=2,即x2+y2=1,
记α为直线B1P与直线BC1所成的角,则α即为直线B1P与直线AD1所成的角,
∴cos<$\overrightarrow{P{B}_{1}}$,$\overrightarrow{B{C}_{1}}$>=$\frac{\overrightarrow{P{B}_{1}}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{P{B}_{1}}||\overrightarrow{B{C}_{1}}|}$=$\frac{3\sqrt{2}x}{2×3\sqrt{2}}$=$\frac{x}{2}$,
∵点P的轨迹在平面A1BC1内是以O为圆心,1为半径的单位圆,
∴-1≤x≤1,∴-$\frac{1}{2}$≤cos<$\overrightarrow{P{B}_{1}}$,$\overrightarrow{B{C}_{1}}$>≤$\frac{1}{2}$,
又∵α为锐角,∴0≤cos<$\overrightarrow{P{B}_{1}}$,$\overrightarrow{B{C}_{1}}$>≤$\frac{1}{2}$,
故选:A.
点评 本题考查求空间中线线角的三角函数值,建立恰当的坐标系是解决本题的关键,注意解题方法的积累,属于难题.

| A. | 4 | B. | 8 | C. | 9 | D. | 12 |
| A. | ($\sqrt{2}$-1)2 | B. | 2($\sqrt{2}$+1)2 | C. | 3($\sqrt{2}$-1)2 | D. | 4($\sqrt{2}$+1)2 |
 如图,过圆O外一点A分别作圆O的两条切线AB、AC,延长BA于点D,使DA=AB,直线CD交圆O于点E,AE交圆O于点F,交BC于点I,AC与DF交于点H.
如图,过圆O外一点A分别作圆O的两条切线AB、AC,延长BA于点D,使DA=AB,直线CD交圆O于点E,AE交圆O于点F,交BC于点I,AC与DF交于点H. 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),A(2,0)是长轴的一个端点,弦BC过椭圆的中心O,且$\overrightarrow{AC}$$•\overrightarrow{BC}$=0,|$\overrightarrow{OC}-\overrightarrow{OB}|$=2|$\overrightarrow{BC}-\overrightarrow{BA}$|.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),A(2,0)是长轴的一个端点,弦BC过椭圆的中心O,且$\overrightarrow{AC}$$•\overrightarrow{BC}$=0,|$\overrightarrow{OC}-\overrightarrow{OB}|$=2|$\overrightarrow{BC}-\overrightarrow{BA}$|. 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=2BE=4.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=2BE=4.