题目内容
12. 如图,过圆O外一点A分别作圆O的两条切线AB、AC,延长BA于点D,使DA=AB,直线CD交圆O于点E,AE交圆O于点F,交BC于点I,AC与DF交于点H.
如图,过圆O外一点A分别作圆O的两条切线AB、AC,延长BA于点D,使DA=AB,直线CD交圆O于点E,AE交圆O于点F,交BC于点I,AC与DF交于点H.(Ⅰ)证明:A、D、C、F四点共圆.
(Ⅱ)若HI∥DE,求证:△BED为等腰直角三角形.
分析 (Ⅰ)连接CF,证明∠CFE=∠BDC,即可证明A、D、C、F四点共圆.
(Ⅱ)证明∠ADC=∠DBC=∠CBE,BC⊥DE,即可证明△BED为等腰直角三角形.
解答  证明:(Ⅰ)连接CF,由已知,在△BCD中,AB=AC=AD,
证明:(Ⅰ)连接CF,由已知,在△BCD中,AB=AC=AD,
∴∠BCD=∠BCE=90°,
∴BE是圆O的直径.---------------------(2分)
∵∠CBE+∠DBC=90°,∠BDC+∠DBC=90°,
∴∠BDC=∠CBE.
∵∠CBE=∠CFE,
∴∠CFE=∠BDC,
∴A、D、C、F四点共圆.----------------------------------------------------(5分)
(Ⅱ)连接HI,BF,由(Ⅰ)A、D、C、F四点共圆.得∠ADF=∠ACF=∠FBC,
∵AC是圆O的切线,
∴∠ACF=∠CEF,
∵HI∥DE,
∴∠CEF=∠HIF=∠HCF,
∴H、C、I、F四点共圆.-----------------------------------------------------------(3分)
∴∠HDC=∠FHI=∠FCI=∠ABF,
∴∠ADC=∠DBC=∠CBE,
又BC⊥DE,
∴△BED为等腰直角三角形.--------------------------------------------------------(5分)
点评 本题考查四点共圆的证明与性质的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某地区有小学18所,中学12所,大学6所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
根据前四个年级的数据,利用最小二乘法求y关于x的线性回归直线方程,并计算五年级近视眼率的估计值与实际值之间的差的绝对值.
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
| 年级号x | 1 | 2 | 3 | 4 | 5 |
| 近视眼率y | 0.1 | 0.15 | 0.2 | 0.3 | 0.39 |
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
8.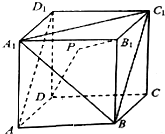 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{3}$] | C. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |