设非负实数x.y满足约束条件$\left\{\begin{array}{l}x+y-3{≤} {\;}0{.} {\;}\\ 2x+y-4{≥} {\;}0\end{array}\right.$则z=2x+3y的最大值为( )A．4B．8C．9D．12 题目和参考答案——青夏教育精英家教网—

题目内容

11．设非负实数x，y满足约束条件$\left\{\begin{array}{l}x+y-3{≤}_{\;}0{，}_{\;}\\ 2x+y-4{≥}_{\;}0\end{array}\right.$则z=2x+3y的最大值为（　　）

A．

B．

C．

D．

分析令2x+3y=m（x+y）+n（2x+y），则$\left\{\begin{array}{l}{m+2n=2}\\{m+n=3}\end{array}\right.$，可得m=4，n=-1，结合条件，即可求出z=2x+3y的最大值．

解答解：令2x+3y=m（x+y）+n（2x+y），则
$\left\{\begin{array}{l}{m+2n=2}\\{m+n=3}\end{array}\right.$，∴m=4，n=-1，
∴2x+3y=4（x+y）-（2x+y）≤12-4=8，
∴z=2x+3y的最大值为8，
故选：B．

点评本题考查目标函数的最大值，考查学生的计算能力，正确运用待定系数法是解题的关键．

练习册系列答案

18．已知数列{a_n}满足：a₁=$\frac{3}{2}$，且a_n=$\frac{3n{a}_{n-1}}{2{a}_{n-1}+n-1}$（n≥2，n∈N^*），求数列{a_n}的通项公式．

6．在平面直角坐标系xoy中，设点P（x₀，y₀）为椭圆Γ：$\frac{x^2}{4}+\frac{y^2}{3}=1$上一点，过点P的直线${l_1}：\frac{{{x_0}x}}{4}+\frac{{{y_0}y}}{3}=1$交直线l₂：x=4于点Q．
（1）证明：直线l₁为椭圆Γ的切线；
（2）x轴上是否存在定点R，使得以PQ为直径的圆过定点R？若存在，求出R的坐标，若不存在，说明理由．

16．已知a∈N，b∈N，且$\frac{1}{a}$+$\frac{10}{b}$=1，则当a=11，b=11时，a+b最小．

3．已知直线l：y=x+2与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）相交于B、D两点，且BD的中点为M（1，3）．
（1）求双曲线C的离心率；
（2）设双曲线C的右顶点为A，右焦点为F，|BF|•|DF|=17，试判断△ABD是否为直角三角形，并说明理由．

20．设等差数列{a_n}的前n项和为S_n，满足：a₂+a₄=18，S₇=91．递增的等比数列{b_n}前n项和为T_n，满足：b₁+b_k=66，b₂b_k-1=128，T_k=126，
（1）求{a_n}、{b_n}的通项公式
（2）设数列{c_n}对?n∈N⁺，均有$\frac{c_1}{b_1}+\frac{c_2}{b_2}+…+\frac{c_n}{b_n}={a_{n+1}}$成立，求c₁+c₂+…+c₂₀₁₅．

8．

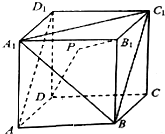如图，在棱长为3的正方体ABCD-A₁B₁C₁D₁中，点P是平面A₁BC₁内一动点，且满足|PD|+|PB₁|=2+$\sqrt{13}$，则直线B₁P与直线AD₁所成角的余弦值的取值范围为（　　）

[$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$]

D．

[$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$]

试题分类