题目内容
3. 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),A(2,0)是长轴的一个端点,弦BC过椭圆的中心O,且$\overrightarrow{AC}$$•\overrightarrow{BC}$=0,|$\overrightarrow{OC}-\overrightarrow{OB}|$=2|$\overrightarrow{BC}-\overrightarrow{BA}$|.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),A(2,0)是长轴的一个端点,弦BC过椭圆的中心O,且$\overrightarrow{AC}$$•\overrightarrow{BC}$=0,|$\overrightarrow{OC}-\overrightarrow{OB}|$=2|$\overrightarrow{BC}-\overrightarrow{BA}$|.(Ⅰ)求椭圆的方程;
(Ⅱ)设P、Q为椭圆上异于A,B且不重合的两点,且∠PCQ的平分线总是垂直于x轴,是否存在实数λ,使得$\overrightarrow{PQ}$=λ$\overrightarrow{AB}$,若存在,请求出λ的最大值,若不存在,请说明理由.
分析 (Ⅰ)由已知条件推导出△AOC是等腰直角三角形,C(1,1),由点C在椭圆上,得$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1,a=2$,由此能求出椭圆方程.
(Ⅱ)对于椭圆上两点P,Q,由∠PCQ的平分线总是垂直于x轴,知PC与CQ所在直线关于x=1对称,kPC=k,则kCQ=-k,PC的直线方程为y=k(x-1)+1,QC的直线方程为y=-k(x-1)+1,由此求出PQ∥AB,从而得到存在实数λ,使得$\overrightarrow{PQ}$=λ$\overrightarrow{AB}$,求出|$\overrightarrow{PQ}$|的最大值,即可得出结论.
解答 解:(I)∵$\overrightarrow{AC}$$•\overrightarrow{BC}$=0,∴∠ACB=90°,
又|$\overrightarrow{OC}-\overrightarrow{OB}|$=2|$\overrightarrow{BC}-\overrightarrow{BA}$|,即|$\overrightarrow{BC}$|=2|$\overrightarrow{AC}$|,
∴△AOC是等腰直角三角形 …(2分)
∵A(2,0),∴C(1,1),
而点C在椭圆上,∴$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1,a=2$
∴b2=$\frac{4}{3}$,
∴所求椭圆方程为$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$; …(4分)
(II)对于椭圆上两点P,Q,
∵∠PCQ的平分线总是垂直于x轴,
∴PC与CQ所在直线关于x=1对称,
kPC=k,则kCQ=-k,…(6分)
∵C(1,1),∴PC的直线方程为y=k(x-1)+1,①
QC的直线方程为y=-k(x-1)+1,②
将①代入$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$得(1+3k2)x2-6k(k-1)x+3k2-6k-1=0,③
∵C(1,1)在椭圆上,∴x=1是方程③的一个根,∴xP=$\frac{3{k}^{2}-6k-1}{1+3{k}^{2}}$…(8分)
以-k替换k,得到xQ=$\frac{3{k}^{2}+6k-1}{3{k}^{2}+1}$.
∴kPQ=$\frac{k({x}_{P}+{x}_{Q})-2k}{{x}_{P}-{x}_{Q}}$=$\frac{1}{3}$
∵∠ACB=90°,A(2,0),C(1,1),弦BC过椭圆的中心O,
∴A(2,0),B(-1,-1),∴kAB=$\frac{1}{3}$,
∴kPQ=kAB,∴PQ∥AB,
∴存在实数λ,使得$\overrightarrow{PQ}$=λ$\overrightarrow{AB}$ …(10分)
|$\overrightarrow{PQ}$|=$\sqrt{(\frac{-12k}{1+3{k}^{2}})^{2}+(\frac{-4k}{1+3{k}^{2}})^{2}}$=$\sqrt{\frac{160}{9{k}^{2}+\frac{1}{{k}^{2}}+6}}$≤$\frac{2\sqrt{30}}{3}$
当$9{k}^{2}=\frac{1}{{k}^{2}}$时即k=±$\frac{\sqrt{3}}{3}$时取等号,
又|$\overrightarrow{AB}$|=$\sqrt{10}$,λmax=$\frac{\frac{2\sqrt{30}}{3}}{\sqrt{10}}$=$\frac{2\sqrt{3}}{3}$ …(13分)
点评 本题考查椭圆方程的求法,考查满足条件的实数是否存在的判断与求法,考查直线与椭圆的位置关系,属于中档题.

(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
| 年级号x | 1 | 2 | 3 | 4 | 5 |
| 近视眼率y | 0.1 | 0.15 | 0.2 | 0.3 | 0.39 |
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
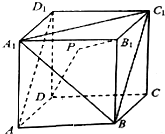 如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )
如图,在棱长为3的正方体ABCD-A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+$\sqrt{13}$,则直线B1P与直线AD1所成角的余弦值的取值范围为( )| A. | [0,$\frac{1}{2}$] | B. | [0,$\frac{1}{3}$] | C. | [$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |