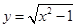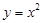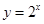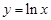题目内容
设函数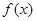 的定义域为
的定义域为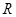 ,若存在常数
,若存在常数 ,使
,使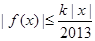 对一切实数
对一切实数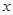 均成立
均成立
,则称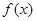 为“好运”函数.给出下列函数:
为“好运”函数.给出下列函数:
①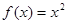 ;②
;② ;③
;③ ;④
;④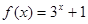 .
.
其中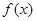 是“好运”函数的序号为 .
是“好运”函数的序号为 .
| A.① ② | B.① ③ | C.③ | D.②④ |
C
解析试题分析:对于①,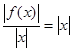 ,显然不存在常数
,显然不存在常数 ,使得
,使得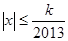 ,故不满足题意.
,故不满足题意.
对于②, ,由于
,由于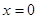 时,
时,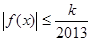 不成立,故错误;
不成立,故错误;
对于③,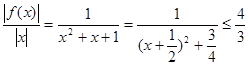 ,令
,令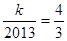 ,则
,则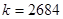 ,使
,使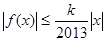 对一切实数
对一切实数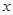 均成立.故③正确.
均成立.故③正确.
对于④,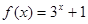 ,由于
,由于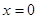 时,
时,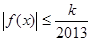 不成立,故错误.
不成立,故错误.
考点:函数恒成立问题
点评:本题考查阅读题意的能力,考查学生对新定义的理解,根据“好运”的定义进行判定
是关键.

练习册系列答案
相关题目
定义在 上的偶函数
上的偶函数 满足:对任意的
满足:对任意的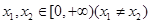 ,有
,有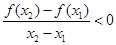 .则
.则
A.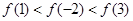 | B.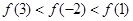 |
C.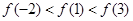 | D. |
函数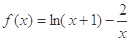 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.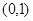 | B.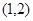 | C.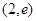 | D.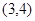 |
函数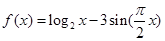 零点的个数是 ( )
零点的个数是 ( )
| A.5 | B.4 | C.3 | D.2 |
函数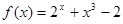 在区间(0,1)内的零点个数是 ( )
在区间(0,1)内的零点个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
已知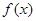 是定义在R上的偶函数,在区间
是定义在R上的偶函数,在区间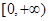 上为增函数,且
上为增函数,且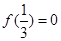 ,则不等式
,则不等式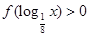 的解集为( )
的解集为( )
A.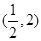 | B.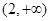 |
C.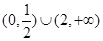 | D.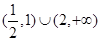 |
已知定义在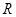 上的偶函数
上的偶函数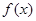 满足
满足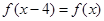 ,且在区间[0,2]上
,且在区间[0,2]上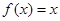 ,若关于
,若关于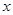 的方程
的方程 有三个不同的根,则
有三个不同的根,则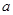 的范围为
的范围为
A.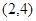 | B.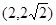 | C.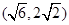 | D.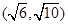 |

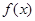 ,如果存在锐角
,如果存在锐角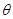 使得
使得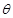 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数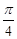 的旋转性的是( )
的旋转性的是( )