题目内容
对于函数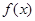 ,如果存在锐角
,如果存在锐角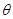 使得
使得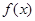 的图象绕坐标原点逆时针旋转角
的图象绕坐标原点逆时针旋转角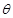 ,所得曲线仍是一函数,则称函数
,所得曲线仍是一函数,则称函数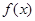 具备角
具备角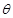 的旋转性,下列函数具有角
的旋转性,下列函数具有角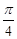 的旋转性的是( )
的旋转性的是( )
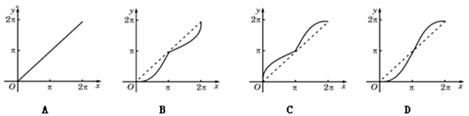
A.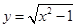 | B.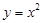 | C.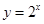 | D. |
A
解析试题分析:根据图像的旋转定义,满足存在锐角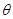 使得
使得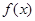 的图象绕坐标原点逆时针旋转角
的图象绕坐标原点逆时针旋转角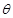 ,所得曲线仍是一函数,则函数
,所得曲线仍是一函数,则函数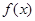 具备角
具备角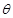 的旋转性,对于选项B,由于只要旋转的锐角为
的旋转性,对于选项B,由于只要旋转的锐角为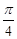 则可知不是函数,对与选项C,结合指数函数的图像可知,做
则可知不是函数,对与选项C,结合指数函数的图像可知,做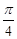 的旋转,必然与x=a有两个交点不成立,对于选项D,同样可知由于在x=1处的导数值为1,那么可知旋转后不是函数,因此可知选A.
的旋转,必然与x=a有两个交点不成立,对于选项D,同样可知由于在x=1处的导数值为1,那么可知旋转后不是函数,因此可知选A.
考点:函数图像的旋转
点评:主要是考查了向量的运用,结合图像进行旋转来分析得到结论,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若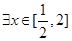 ,使
,使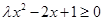 成立,则实数
成立,则实数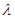 的取值范围为( )
的取值范围为( )
A.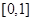 | B.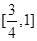 | C. | D.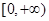 |
设函数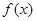 的定义域为
的定义域为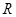 ,若存在常数
,若存在常数 ,使
,使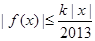 对一切实数
对一切实数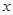 均成立
均成立
,则称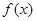 为“好运”函数.给出下列函数:
为“好运”函数.给出下列函数:
①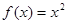 ;②
;② ;③
;③ ;④
;④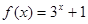 .
.
其中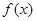 是“好运”函数的序号为 .
是“好运”函数的序号为 .
| A.① ② | B.① ③ | C.③ | D.②④ |
如图是导函数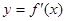 的图像,则下列命题错误的是( )
的图像,则下列命题错误的是( )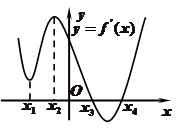
A.导函数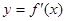 在 在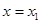 处有极小值 处有极小值 |
B.导函数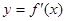 在 在 处有极大值 处有极大值 |
C.函数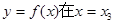 处有极小值 处有极小值 |
D.函数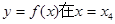 处有极小值 处有极小值 |
已知关于x的函数y=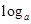 (2-ax)在[0,1]上是减函数,则a的取值范围是
(2-ax)在[0,1]上是减函数,则a的取值范围是
| A.(0,1) | B.(1,2) | C.(0,2) | D.[2,+∞)] |
设函数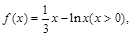 则
则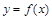 ( )
( )
A.在区间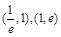 内均有零点 内均有零点 |
B.在区间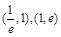 内均无零点 内均无零点 |
C.在区间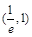 内无零点,在区间 内无零点,在区间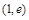 内有零点 内有零点 |
D.在区间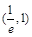 内有零点,在区间 内有零点,在区间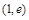 内无零点 内无零点 |
若关于 的方程
的方程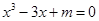 在
在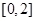 上有根,则实数
上有根,则实数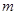 的取值范围是 ( )
的取值范围是 ( )
A.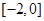 | B.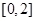 | C.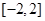 | D. |
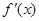 是
是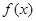 的导函数,
的导函数,
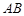 的长为
的长为 ,
,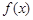 表示弧
表示弧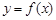 的图象是( )
的图象是( )