题目内容
6.设a为实数,已知函数f(x)=$\frac{1}{3}$x3-ax2+(a2-1)x.(1)当a=1时,求函数f(x)的极值;
(2)若方程f(x)=0有三个不等实数根,求实数a的取值范围.
分析 (1)求得a=1的导数,求得单调区间,即可得到极值;
(2)求得导数,求得单调区间,可得极值,由题意可得极大值大于0,极小值小于0,解不等式即可得到a的范围.
解答 解:(1)函数f(x)=$\frac{1}{3}$x3-x2的导数为f′(x)=x2-2x,
当x>2或x<0时,f′(x)>0,f(x)递增;
当0<x<2时,f′(x)<0,f(x)递减.
即有x=0处取得极大值,且为0;
x=2处取得极小值,且为-$\frac{4}{3}$;
(2)函数f(x)=$\frac{1}{3}$x3-ax2+(a2-1)x的导数为
f′(x)=x2-2ax+a2-1=(x-a+1)(x-a-1),
当x>a+1或x<a-1时,f′(x)>0,f(x)递增;
当a-1<x<a+1时,f′(x)<0,f(x)递减.
即有x=a-1处取得极大值,且为$\frac{1}{3}$(a-1)2(a+2);
x=a+1处取得极小值,且为$\frac{1}{3}$(a+1)2(a-2).
方程f(x)=0有三个不等实数根,
即有$\frac{1}{3}$(a-1)2(a+2)>0,且$\frac{1}{3}$(a+1)2(a-2)<0,
解得-2<a<2,且a≠1,a≠-1.
则实数a的取值范围是(-2,-1)∪(-1,1)∪(1,2).
点评 本题考查导数的运用:求单调区间和极值,考查函数的零点的求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
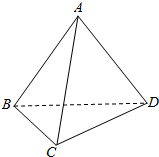 如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.
如图,在三棱锥A-BCD中,AB=BC=CD=DA=AC,BD=$\sqrt{2}$AB,求证:平面ABD⊥平面BCD.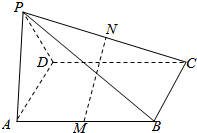 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.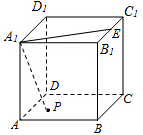 如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.
如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.