题目内容
17．四面体的一条棱长为x，其余棱长均为3，当该四面体体积最大时的表面积为$\frac{9\sqrt{3}}{2}+\frac{9}{4}\sqrt{15}$．分析 判断几何体体积最大时的结构特征，然后利用四面体的表面积就是表面四个三角形的面积和，可直接运用三角形的面积求解．
解答 解：△ABC和△BCD都是边长为3的正三角形，
三棱锥的体积的最大值，是A到底面的距离最大时取得，就是侧面ABC与底面BCD垂直时取得最大值．此时
△ABD和△ACD是全等的等腰三角形，其腰长为3，底边长为x=$\frac{3\sqrt{6}}{2}$，
∴S△ABC=S△BCD=$\frac{\sqrt{3}}{4}×{3}^{2}$=$\frac{9\sqrt{3}}{4}$，
S△ABD=S△ACD=$\frac{1}{2}×\frac{3\sqrt{6}}{2}×\sqrt{9-（\frac{3\sqrt{6}}{4}）^{2}}$=$\frac{9}{8}\sqrt{15}$，
∴当四面体的体积最大时，其表面积S=$\frac{9\sqrt{3}}{2}+\frac{9}{4}\sqrt{15}$．
故答案为：$\frac{9\sqrt{3}}{2}+\frac{9}{4}\sqrt{15}$．
点评 本题考查了棱锥的体积和表面积，考查了学生的空间想象能力和数学转化能力，此题是中档题．
练习册系列答案
字词句段篇系列答案
相关题目
如图，棱长为a的正方体ABCD-A1B1C1D1中，E、F分别为AB和BC的中点，M为棱B1B的中点．求证：
5．若命题p：?x∈R，x＞lnx-2，命题q：?x∈R，2x＞1，那么（ ）
| A． | 命题“p或q”为假 | B． | 命题“p且q“为真 | ||
| C． | 命题，“￢p或q”为假 | D． | 命题“p且￢q“为假 |
2．
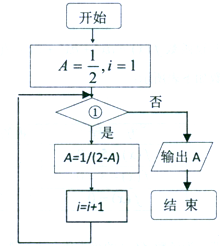如图所示的程序框图，若执行后的结果是$\frac{5}{6}$，则在①处应填写的是（ ）
如图所示的程序框图，若执行后的结果是$\frac{5}{6}$，则在①处应填写的是（ ）| A． | i≤3 | B． | i≤4 | C． | i≤5 | D． | i≤6 |
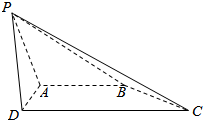如图，四棱锥P-ABCD中，底面ABCD为梯形，AB∥CD．AD⊥CD，CD=2AB=2AD=4，侧面PAD为正三角形，AB⊥PA．