题目内容
【题目】如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中, ![]() 是
是![]() 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
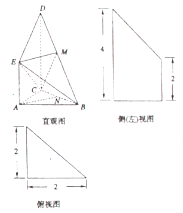
(1)求出该几何体的体积;
(2)若![]() 是
是![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
【答案】(1) ![]() ;(2) 见解析.
;(2) 见解析.
【解析】试题分析:(1)先由面面垂直的性质定理证明![]() ,再由面面垂直的判定定理证明
,再由面面垂直的判定定理证明![]() 证明平面
证明平面![]() ,从而由棱锥的体积公式可得结果;(2)连接
,从而由棱锥的体积公式可得结果;(2)连接![]() ,由中位线定理得
,由中位线定理得![]() ,由平行四边形可得
,由平行四边形可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(1)由题意可知:四棱锥![]() 中,
中,
平面![]() 平面
平面![]() ,
, ![]()
平面![]() 平面
平面![]()
所以, ![]() 平面
平面![]()
又![]() ,
, ![]() ,
,
则四棱锥![]() 的体积为:
的体积为: ![]()
(2)连接![]() ,则
,则![]() ,
, ![]()
又![]() ,所以四边形
,所以四边形![]() 为平心四边形,
为平心四边形, ![]()
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以, ![]() 平面
平面![]()
【方法点晴】本题主要考查线面平行的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用![]() 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.