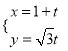题目内容
【题目】已知函数
，
，
（1）当
时，求曲线
在点
处的切线方程；
（2）讨论函数
的单调性并判断有无极值，有极值时求出极值.
【答案】（1）
;（2）见解析.
【解析】试题分析：（1）欲求曲线
在点
处的切线方程，只需求出斜率
和和
的值，即可利用直线的点斜式方程求解切线的方程；
（2）求出
，通过讨论
的取值范围，求出函数的单调区间，从而求出函数的极值即可，可分
两种情况，求出函数的单调区间，得出函数的极值.
试题解析：
（1）
时，
，
所以
，
因此曲线在点
处的切线方程是
即
（2）
①当
时，
恒成立，
所以当
时
，
单调递减
当
时，
，单调递增
所以当
时，取极小值
②当
时，由
得
或
（ⅰ）当
，即
时
由得
或
由得
所以在
上单调递增，在
上单调递减，在
上单调递增，故时，取极大值，
时，取极小值
（ⅱ）当
，即
时，
恒成立
此时函数在
上单调递增，函数无极值
（ⅲ）当
，即
时
由得
或
由得
所以在
上单调递增，在
上单调递减，在
上单调递增，故时，取极大值
时，取极小值.
练习册系列答案
相关题目
【题目】某单位实行休年假制度三年以来，50名职工休年假的次数进行的调查统计结果如下表所示：
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题：
（1）从该单位任选两名职工，求这两人休年假次数之和为4的概率；
（2）从该单位任选两名职工，用
表示这两人休年假次数之差的绝对值，求随机变量
的分布列及数学期望
．
