题目内容
设数列{an}的前n项和Sn满足 =3n-2.
=3n-2.
(1)求数列{an}的通项公式;
(2)设bn= ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
 =3n-2.
=3n-2.(1)求数列{an}的通项公式;
(2)设bn=
 ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.(1)an=6n-5(n∈N*)
(2)10
(2)10
解:(1)由 =3n-2,得Sn=3n2-2n.
=3n-2,得Sn=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-[3(n-1)2-2(n-1)]=6n-5;
当n=1时,a1=S1=3×1-2=6-5=1.
所以an=6n-5(n∈N*).
(2)由(1)得bn= =
= =
= (
( -
- ),
),
故Tn= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=
)]= (1-
(1- ).
).
因此,使得 (1-
(1- )<
)< (n∈N*)成立的m必须满足
(n∈N*)成立的m必须满足 ≤
≤ ,即m≥10,故满足要求的最小正整数m为10.
,即m≥10,故满足要求的最小正整数m为10.
 =3n-2,得Sn=3n2-2n.
=3n-2,得Sn=3n2-2n.当n≥2时,an=Sn-Sn-1=(3n2-2n)-[3(n-1)2-2(n-1)]=6n-5;
当n=1时,a1=S1=3×1-2=6-5=1.
所以an=6n-5(n∈N*).
(2)由(1)得bn=
 =
= =
= (
( -
- ),
),故Tn=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=
)]= (1-
(1- ).
).因此,使得
 (1-
(1- )<
)< (n∈N*)成立的m必须满足
(n∈N*)成立的m必须满足 ≤
≤ ,即m≥10,故满足要求的最小正整数m为10.
,即m≥10,故满足要求的最小正整数m为10.
练习册系列答案
相关题目
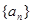 满足
满足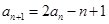 (
(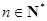 ).
).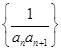 的前
的前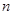 项和
项和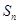 ;
;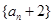 不可能是等比数列.
不可能是等比数列.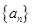 的前
的前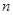 项和
项和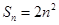 ,
,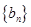 为等比数列,且
为等比数列,且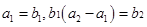 .
.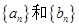 的通项公式;(2)设
的通项公式;(2)设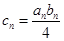 ,求数列
,求数列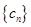 前
前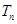 .
.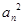 -an+1=an-1(n≥2,n∈N*),则S2014的值为( )
-an+1=an-1(n≥2,n∈N*),则S2014的值为( ) 满足
满足 (
( 为常数,
为常数, )
) 时,求
时,求 ;
; 时,求
时,求 的值;
的值; 恒成立的常数
恒成立的常数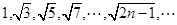 ,则
,则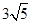 是它的( )
是它的( )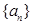 是等差数列,若
是等差数列,若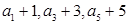 构成公比为
构成公比为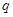 的等比数列,则
的等比数列,则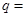 ________.
________.