题目内容
已知数列 满足
满足 (
( 为常数,
为常数, )
)
(1)当 时,求
时,求 ;
;
(2)当 时,求
时,求 的值;
的值;
(3)问:使 恒成立的常数
恒成立的常数 是否存在?并证明你的结论.
是否存在?并证明你的结论.
 满足
满足 (
( 为常数,
为常数, )
)(1)当
 时,求
时,求 ;
;(2)当
 时,求
时,求 的值;
的值;(3)问:使
 恒成立的常数
恒成立的常数 是否存在?并证明你的结论.
是否存在?并证明你的结论.(1) (2)
(2) (3)存在常数
(3)存在常数 ,使
,使 恒成立.
恒成立.
 (2)
(2) (3)存在常数
(3)存在常数 ,使
,使 恒成立.
恒成立.试题分析:假设题型中,先假设存在,然后在该假设下根据题中的已知条件去求值或证明,如果最后可得到数值或证明,则说明存在,否则不存在;分类讨论.
(1)当
 时,根据已知条件
时,根据已知条件 可判断出其符合等差数列的等差中项公式,所以知该数列是等差数列,此时根据题中所给的该数列的前两项,可求出公差,进而利用等差数列的通项公式
可判断出其符合等差数列的等差中项公式,所以知该数列是等差数列,此时根据题中所给的该数列的前两项,可求出公差,进而利用等差数列的通项公式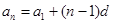 ,求出通项
,求出通项 .
.(2)该题只是给出了数列的前两项和一个递推公式,而此时如果求数列的通项会相当的繁琐,困难.观察题目会发现,要求的是当
 时的第
时的第 项,项数很大,所以猜想该数列的各项之间必然有一定的规律,故不妨列出数列的若干项观察规律,会发现该数列是一个周期为6的数列.有了初步判断之后,可以根据
项,项数很大,所以猜想该数列的各项之间必然有一定的规律,故不妨列出数列的若干项观察规律,会发现该数列是一个周期为6的数列.有了初步判断之后,可以根据 ,找到
,找到 ,最终得到
,最终得到 ,从而证明开始的猜想,然后根据
,从而证明开始的猜想,然后根据 ,可以得出结论
,可以得出结论 ,进而求出
,进而求出 .
.(3)首先假设存在,然后在该假设下根据题中的已知条件去求
 ,如果最后可得到常数
,如果最后可得到常数 ,则说明存在,否则不存在.根据
,则说明存在,否则不存在.根据 ①,可得
①,可得 ②;根据及
②;根据及 ,可得
,可得 ③; 将③带入②有
③; 将③带入②有 ④,此时①④式子含有相同的项,所以1式减④式得
④,此时①④式子含有相同的项,所以1式减④式得 .分别讨论
.分别讨论 或
或 是否成立,并最终形成结论.
是否成立,并最终形成结论.(1)当
 时,根据题意可知
时,根据题意可知 成立,显然该式符合等差数列的等差中项公式,
成立,显然该式符合等差数列的等差中项公式,所以该数列是等差数列,根据题意首项为
 ,公差为
,公差为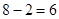 ,
,根据差数列的通项公式
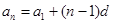 可知
可知 .
.(2)根据题意列出该数列的一些项,如下:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,我们发现该数列为一周期为6的数列.
事实上,根据题意可知,
 ,则有
,则有 ①
①又因为
 有
有 ②
②将②带入①化简得
 ③;
③;根据③式有
 ,
,所以说明该数列是周期为6的数列.
因为
 ,所以
,所以 .
.(3)假设存在常数
 ,使
,使 恒成立.
恒成立.由
 ①,可得
①,可得 ②,
②,及
 ,可得
,可得 ③
③将③带入②有
 ④
④ ①式减④式得
 .
.所以
 ,或
,或 .
.当
 ,
, 时,数列{
时,数列{ }为常数数列,显然不满足题意.
}为常数数列,显然不满足题意.由
 得
得 ,于是
,于是 ,
,即对于
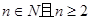 ,都有
,都有 ,
,所以
 ,从而
,从而
 .
.所以存在常数
 ,使
,使 恒成立.
恒成立.
练习册系列答案
相关题目
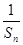 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[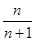 +
+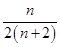 ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由. =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. 的公差
的公差 ,且
,且 成等比数列,则
成等比数列,则 的值是_______.
的值是_______. }满足
}满足 +
+ )
) ,
, ,
, 的值;
的值; 的前
的前 项和为
项和为 ,且对任意的
,且对任意的 ,都有
,都有 。
。 满足
满足 ,且cn=anbn,求数列
,且cn=anbn,求数列 的前
的前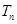 ;
; ,使得对任意的正整数
,使得对任意的正整数 ,若存在,求出
,若存在,求出 中,a1=1,d=3,an=298,则n的值等于( ).
中,a1=1,d=3,an=298,则n的值等于( ).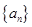 中,
中,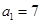 ,公差为
,公差为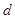 ,前
,前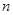 项和为
项和为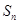 ,当且仅当
,当且仅当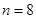 时
时