题目内容
11. 设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.
设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.(Ⅰ)求φ;
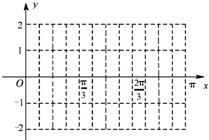
(Ⅱ)在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(Ⅲ)求函数f(x)≥1(x∈R)的解集.
分析 (Ⅰ)根据函数的对称中心代入即可求φ;
(Ⅱ)利用五点法即可在给定的平面直角坐标系中作出该函数在x∈[0,π]的图象;
(Ⅲ)结合三角不等式进行求解即可.
解答  解:(Ⅰ)∵$(\frac{π}{3},0)$是函数y=f(x)的图象的对称中心,
解:(Ⅰ)∵$(\frac{π}{3},0)$是函数y=f(x)的图象的对称中心,
∴$2sin(2×\frac{π}{3}+φ)=0$,∴$\frac{2π}{3}+φ=kπ(k∈Z)$,
∴$φ=kπ-\frac{2π}{3}$∵0<φ<π,∴$φ=\frac{π}{3}$,
即$f(x)=2sin({2x+\frac{π}{3}})$.
(Ⅱ)列表
| x | 0 | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | π |
| $2x+\frac{π}{3}$ | $\frac{π}{3}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{7π}{3}$ |
| f(x) | $\sqrt{3}$ | 2 | 0 | -2 | 0 | $\sqrt{3}$ |
即$2sin(2x+\frac{π}{3})≥1$$sin(2x+\frac{π}{3})≥\frac{1}{2}$,$\frac{π}{6}+2kπ≤2x+\frac{π}{3}≤\frac{5π}{6}+2kπ,k∈Z$.
∴$-\frac{π}{12}+kπ≤x≤\frac{π}{4}+kπ,k∈Z$,
求函数f(x)≥1(x∈R)的解集是$x∈[-\frac{π}{12}+kπ,\frac{π}{4}+kπ],k∈Z$.
点评 本题主要考查三角函数的图象和性质,根据条件求出φ的值是解决本题的关键.

练习册系列答案
相关题目
1.函数f(x)=$\sqrt{3}$cos4x+sin4x(x∈R)的递减区间为( )
| A. | $[-\frac{5π}{24}+\frac{1}{2}kπ,\frac{π}{24}+\frac{1}{2}kπ](k∈Z)$ | B. | [$\frac{π}{24}+\frac{1}{2}kπ$,$\frac{7π}{24}+\frac{1}{2}kπ$](k∈Z | ||
| C. | [-$\frac{π}{6}$+$\frac{1}{2}$Kπ,$\frac{π}{12}+\frac{1}{2}kπ$](k∈Z) | D. | [$\frac{π}{12}+\frac{1}{2}kπ$,$\frac{π}{3}$+$\frac{1}{2}$kπ](k∈Z) |
19.化简sin420°的值是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16. 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
 如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )
如图,设A,B两点在河的两岸,一测量者在点A所在的同侧河岸边选定一点C,测出AC的距离为100m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( )| A. | 100$\sqrt{3}$ m | B. | 100$\sqrt{2}$ m | C. | 50$\sqrt{2}$ m | D. | 25$\sqrt{2}$ m |
20.某几何体的三视图所示,且该几何体的体积是4,则正视图中的x的值是( )
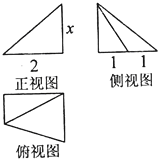

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.复数z=3-i的虚部是( )
| A. | 1 | B. | i | C. | -1 | D. | -i |