题目内容
已知数列{an}的前n项和为Sn,a1=2.当n≥2时,Sn-1+1,an,Sn+1成等差数列.
(1)求证:{Sn+1}是等比数列;
(2)求数列{nan}的前n项和Tn.
(1)求证:{Sn+1}是等比数列;
(2)求数列{nan}的前n项和Tn.
(1)见解析
(2)Tn=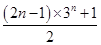
(2)Tn=
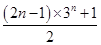
解:(1)证明:∵Sn-1+1,an,Sn+1成等差数列,
∴2an=Sn+Sn-1+2(n≥2).
∴2(Sn-Sn-1)=Sn+Sn-1+2,即Sn=3Sn-1+2,
∴Sn+1=3(Sn-1+1)(n≥2).
∴{Sn+1}是首项为S1+1=3,公比为3的等比数列.
(2)由(1)可知Sn+1=3n,∴Sn=3n-1.
当n≥2时,an=Sn-Sn-1=2×3n-1.
又a1=2,∴an=2×3n-1(n∈N*).nan=2n·3n-1
∴Tn=2+4×3+6×32+…+2(n-1)×3n-2+2n×3n-1,①
3Tn=2×3+4×32+6×33+…+2(n-1)×3n-1+2n×3n,②
由①-②得,
-2Tn=2+2×3+2×32+…+2×3n-1-2n×3n= -2n×3n=3n-1-2n×3n,
-2n×3n=3n-1-2n×3n,
∴Tn=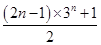 .
.
∴2an=Sn+Sn-1+2(n≥2).
∴2(Sn-Sn-1)=Sn+Sn-1+2,即Sn=3Sn-1+2,
∴Sn+1=3(Sn-1+1)(n≥2).
∴{Sn+1}是首项为S1+1=3,公比为3的等比数列.
(2)由(1)可知Sn+1=3n,∴Sn=3n-1.
当n≥2时,an=Sn-Sn-1=2×3n-1.
又a1=2,∴an=2×3n-1(n∈N*).nan=2n·3n-1
∴Tn=2+4×3+6×32+…+2(n-1)×3n-2+2n×3n-1,①
3Tn=2×3+4×32+6×33+…+2(n-1)×3n-1+2n×3n,②
由①-②得,
-2Tn=2+2×3+2×32+…+2×3n-1-2n×3n=
 -2n×3n=3n-1-2n×3n,
-2n×3n=3n-1-2n×3n,∴Tn=
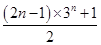 .
.
练习册系列答案
相关题目
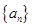 的前
的前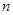 项和
项和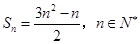 .
.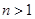 ,都有
,都有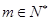 ,使得
,使得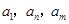 成等比数列.
成等比数列. 满足
满足 则
则 ( )
( ) 和
和 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合 ,集合
,集合 .
. ,
, 时,用列举法表示集合
时,用列举法表示集合 ;
; ,
, ,
, ,其中
,其中 证明:若
证明:若 ,则
,则 .
.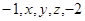 成等比数列,则
成等比数列,则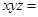 ( )
( )



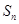 为数列
为数列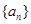 的前
的前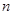 项和,
项和,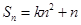 ,
,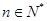 ,其中
,其中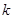 是常数.若对于任意的
是常数.若对于任意的 ,
,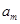 ,
,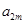 ,
, 成等比数列,则
成等比数列,则