题目内容
在四边形ABCD中,∠ABC=∠BAD=90°,AB=BC=2AD=4,E,F,G分别是BC,CD,AB的中点(如图1).将四边形ABCD沿FG折成空间图形(如图2)后,(1)求证:DE⊥FG;
(2)线段BG上是否存在一点M,使得AM∥平面BDF?若存在,试指出点M的位置,并证明之;若不存在,试说明理由.

【答案】分析:(1)先通过图1得到AD∥BC,再由中位线定理得到FG∥AD∥BC,由图2可得到AD=BE,进而可知四边形ABED是平行四边形,可证明AB∥DE,再由∠GAD=∠GBC=90°,FG∥AD,FG∥BC,可得到AG⊥FG且BG⊥FG,最后根据线面垂直的判定定理可证FG⊥平面AGB,又因为AB?平面AGB,所以DE⊥FG.
(2)先判断当M在线段BG上,且BM=2MG时,AM∥平面BDF.根据等比线段的性质得到 从而知四边形MNDA是平行四边形,
从而知四边形MNDA是平行四边形,
得到AM∥DN,再由线面平行的判定定理可知AM∥平面BDF,得证.
解答:证明:(1)在图1中,因为∠ABC=∠BAD=90°,所以AD∥BC.
因为F,G分别是CD,AB的中点,所以FG∥AD∥BC.
在图2中,因为FG∥AD,FG∥BC,所以AD∥BC.
因为BC=2AD,E是BC的中点,所以AD=BE.
所以四边形ABED是平行四边形.
所以AB∥DE.
因为∠GAD=∠GBC=90°,FG∥AD,FG∥BC,
所以AG⊥FG,且BG⊥FG.
因为AG∩BG=G,且AG,BG?平面AGB,所以FG⊥平面AGB.
因为AB?平面AGB,所以FG⊥AB.
所以DE⊥FG.
(2)当M在线段BG上,且BM=2MG时,AM∥平面BDF.
证明如下:
在线段BF上取点N,使BN=2NF.
因为FG是梯形ABCD的中位线,BC=2AD=4,
所以FG∥AD,且FG=3.
因为BM=2ME,BN=2NF,所以MN∥FG,且MN=
所以
所以四边形MNDA是平行四边形.
所以AM∥DN.
又因为DN?平面BDF,AM?平面BDF,
所以AM∥平面BDF.
点评:本题主要考查线面垂直的判定定理、线面平行的判定定理的应用.考查对立体几何中基本定理的综合应用能力和空间想象能力.
(2)先判断当M在线段BG上,且BM=2MG时,AM∥平面BDF.根据等比线段的性质得到
 从而知四边形MNDA是平行四边形,
从而知四边形MNDA是平行四边形,得到AM∥DN,再由线面平行的判定定理可知AM∥平面BDF,得证.
解答:证明:(1)在图1中,因为∠ABC=∠BAD=90°,所以AD∥BC.
因为F,G分别是CD,AB的中点,所以FG∥AD∥BC.
在图2中,因为FG∥AD,FG∥BC,所以AD∥BC.
因为BC=2AD,E是BC的中点,所以AD=BE.
所以四边形ABED是平行四边形.
所以AB∥DE.
因为∠GAD=∠GBC=90°,FG∥AD,FG∥BC,
所以AG⊥FG,且BG⊥FG.
因为AG∩BG=G,且AG,BG?平面AGB,所以FG⊥平面AGB.
因为AB?平面AGB,所以FG⊥AB.
所以DE⊥FG.
(2)当M在线段BG上,且BM=2MG时,AM∥平面BDF.
证明如下:
在线段BF上取点N,使BN=2NF.
因为FG是梯形ABCD的中位线,BC=2AD=4,
所以FG∥AD,且FG=3.
因为BM=2ME,BN=2NF,所以MN∥FG,且MN=

所以

所以四边形MNDA是平行四边形.
所以AM∥DN.
又因为DN?平面BDF,AM?平面BDF,
所以AM∥平面BDF.
点评:本题主要考查线面垂直的判定定理、线面平行的判定定理的应用.考查对立体几何中基本定理的综合应用能力和空间想象能力.

练习册系列答案
相关题目
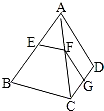 如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则
如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则