题目内容
四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,CD∥AB,AB=4,CD=1,点M在PB上,且MB=3PM,PB与平面ABC成30°角.(1)求证:CM∥面PAD;
(2)求证:面PAB⊥面PAD;
(3)求点C到平面PAD的距离.
分析:根据题意,建立空间直角坐标系O-xyz,C为坐标原点O,
(1)要证CM∥面PAD,只需求出向量
与面PAD内的向量
、
共面即可.
( 2)过B作BE⊥PA,E为垂足.要证面PAB⊥面PAD,只需证明面PAB内的向量
垂直面PAD内的直线PA、DA即可;
(3)利用
在平面PAD的单位向量上的射影,求点C到平面PAD的距离.
(1)要证CM∥面PAD,只需求出向量
| CM |
| DP |
| DA |
( 2)过B作BE⊥PA,E为垂足.要证面PAB⊥面PAD,只需证明面PAB内的向量
| BE |
(3)利用
| SD |
解答: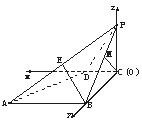 解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,
解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,
(1)证明:如图,建立空间直角坐标系.
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,即∠PBC=30°.
∵|PC|=2,∴|BC|=2
,|PB|=4.
得D(1,0,0)、B(0,2
,0)、
A(4,2
,0)、P(0,0,2).
∵|MB|=3|PM|,
∴|PM|=1,M(0,
,
),
=(0,
,
),
=(-1,0,2),
=(3,2
,0).
设
=x
+y
(x、y∈R),
则(0,
,
)=x(-1,0,2)+y(3,2
,0)?x=
且y=
,
∴
=
+
.
∴
、
、
共面.又∵C∉平面PAD,故CM∥平面PAD.
(2)证明:过B作BE⊥PA,E为垂足.
∵|PB|=|AB|=4,∴E为PA的中点.
∴E(2,
,1),
=(2,-
,1).
又∵
•
=(2,-
,1)•(3,2
,0)=0,
∴
⊥
,即BE⊥DA.
而BE⊥PA,∴BE⊥面PAD.
∵BE?面PAB,∴面PAB⊥面PAD.
(3)解:由BE⊥面PAD知,
平面PAD的单位向量n0=
=
(2,-
,1).
∴CD=(1,0,0)的点C到平面PAD的距离
d=|n0•
|=|
(2,-
,1)•(1,0,0)|=
.
 解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,
解:如图,建立空间直角坐标系O-xyz,C为坐标原点O,(1)证明:如图,建立空间直角坐标系.
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABC所成的角,即∠PBC=30°.
∵|PC|=2,∴|BC|=2
| 3 |
得D(1,0,0)、B(0,2
| 3 |
A(4,2
| 3 |
∵|MB|=3|PM|,
∴|PM|=1,M(0,
| ||
| 2 |
| 3 |
| 2 |
| CM |
| ||
| 2 |
| 3 |
| 2 |
| DP |
| DA |
| 3 |
设
| CM |
| DP |
| DA |
则(0,
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
∴
| CM |
| 3 |
| 4 |
| DP |
| 1 |
| 4 |
| DA |
∴
| CM |
| DP |
| DA |
(2)证明:过B作BE⊥PA,E为垂足.
∵|PB|=|AB|=4,∴E为PA的中点.
∴E(2,
| 3 |
| BE |
| 3 |
又∵
| BE |
| DA |
| 3 |
| 3 |
∴
| BE |
| DA |
而BE⊥PA,∴BE⊥面PAD.
∵BE?面PAB,∴面PAB⊥面PAD.
(3)解:由BE⊥面PAD知,
平面PAD的单位向量n0=
| ||
|
|
| 1 | ||
2
|
| 3 |
∴CD=(1,0,0)的点C到平面PAD的距离
d=|n0•
| CD |
| 1 | ||
2
|
| 3 |
| ||
| 2 |
点评:本题主要考查空间直角坐标系的概念、空间点和向量的坐标表示以及用向量法证明平行关系,同时考查向量研究空间图形的数学思想方法.突破点在于求出相关的向量所对应的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
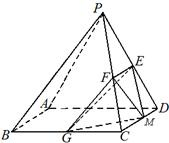 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.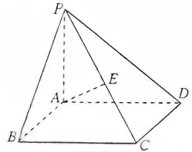 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2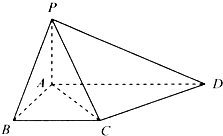 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.