题目内容
【题目】直线
与曲线
相切也与曲线
相切，则称直线为曲线和曲线的公切线，已知函数
，其中
，若曲线和曲线的公切线有两条，则
的取值范围为（ ）
A.
B.
C.
D.
【答案】C
【解析】
设切点求出两个函数的切线方程，根据这个两个方程表示同一直线，可得方程组，化简方程组，可以得到变量
关于其中一个切点横坐标的函数形式，求导，求出函数的单调性，结合该函数的正负性，画出图象图形，最后利用数形结合求出的取值范围.
设曲线
的切点为：
，
，所以过该切点的切线斜率为
，因此过该切点的切线方程为：
；
设曲线
的切点为：
，
，所以过该切点的切线斜率为
，因此过该切点的切线方程为：
，则两曲线的公切线应该满足：
，
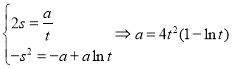构造函数
,
当
时，
单调递减，当
时，
单调递增，所以函数有最大值为：
，当
时，
，当
，
，函数的图象大致如下图所示：
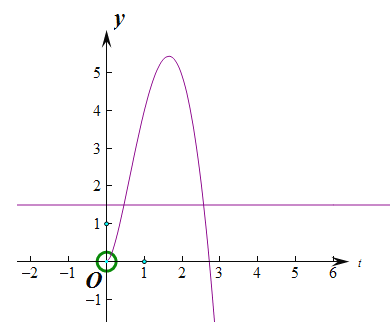
要想有若曲线
和曲线的公切线有两条，则的取值范围为
.
故选：C
练习册系列答案
相关题目
【题目】为了响应国家号召，某校组织部分学生参与了“垃圾分类，从我做起”的知识问卷作答，并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关？
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
（1）是否有90%以上的把握认为“性别”与“问卷的结果”有关？
（2）在成绩合格的学生中，利用性别进行分层抽样，共选取9人进行座谈，再从这9人中随机抽取5人发送奖品，记拿到奖品的男生人数为X，求X的分布列及数学期望
．
附：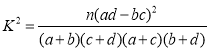
| 0．100 | 0．050 | 0．010 | 0．001 |
| 2．703 | 3．841 | 6．635 | 10．828 |
