题目内容
18.袋中有若干个黑球,3个白球,2个红球(大小形状相同),从中任取2个球,每取到一个黑球得0分,每取到一个白球得1分,每取到一个红球得2分,已知得0分的概率为$\frac{1}{6}$.求(1)袋中黑球的个数;
(2)至少得2分的概率.
分析 (1)先设出袋中黑球个数为x个,通过题意可判断当取到的两球均为黑球时,得分为0分,求出取到两球均为黑球的情况,比上任取两球的情况,即为的0分的概率,据此,解出x的值,
(2)根据互斥事件的概率公式,分别求出得分为0分和1分的概率,计算即可.
解答 解:(1)设袋中黑球的个数为x个,
从袋中任取2个球,共有Cx+52=$\frac{1}{2}$(x+4)(x+5)种不同的取法,
取道两只黑球的情况有Cx2=$\frac{1}{2}$x(x-1)种不同的取法,
而当取到的两球均为黑球时,得分为0分,
∴得0分的概率为$\frac{\frac{1}{2}x(x-1)}{\frac{1}{2}(x+4)(x+5)}$=$\frac{1}{6}$,
∴x=4;
(2)得分小于2分有0分(2个黑球),其概率为$\frac{1}{6}$,1分(1个白球一个黑球),其概率为$\frac{{C}_{3}^{1}•{C}_{4}^{1}}{{C}_{9}^{2}}$=$\frac{1}{3}$,
故至少得2分的概率为1-$\frac{1}{6}$-$\frac{1}{3}$=$\frac{1}{2}$.
点评 本题考查了古典概型概率问题,以及互斥事件的概率问题,属于基础题.

练习册系列答案
相关题目
6.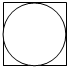 在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
 在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )
在如图的正方形中随机撒一把豆子,用随机模拟的方法估圆周率的值:经查数,落在正方形中的豆子的总数为n粒,其中m(m<n)粒豆子落在该正方形的内切圆内,以此估计圆周率π为( )| A. | $\frac{m}{n}$ | B. | $\frac{2m}{n}$ | C. | $\frac{3m}{n}$ | D. | $\frac{4m}{n}$ |
10.关于z的方程z+i=2+iz的根是( )
| A. | $\frac{3}{2}-\frac{1}{2}$i | B. | $\frac{3}{2}+\frac{1}{2}$i | C. | 3-i | D. | 3+i |
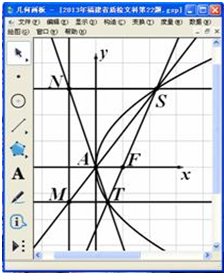 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.