题目内容
已知函数f(x)=ax2+bx+c(a>0),α、β为方程f(x)=x的两根,且0<α<β< ,
,
0<x<α,给出下列不等式,其中成立的是 ( )
①x<f(x) ②α<f(x) ③x>f(x) ④α>f(x)
 ,
,0<x<α,给出下列不等式,其中成立的是 ( )
①x<f(x) ②α<f(x) ③x>f(x) ④α>f(x)
| A.①④ | B.③④ | C.①② | D.②④ |
A
设F(x)=f(x)-x,由 已知α、β是F(x)=0的两根,∴F(x)=a(x-α)(x-β).
已知α、β是F(x)=0的两根,∴F(x)=a(x-α)(x-β).
在x∈(0,α)时,f(x)-x=F(x)=a(x-α)(α-β).
∵a>0,x-α<0,x-β<0,∴F(x)>0.∴f(x)>x.
又a-f(x)=α-[F(x)+x]=α-x-F(x)=α-x-a(x-α)(x-β)=(α- x)[1+a(α-β)].
x)[1+a(α-β)].
∵0<x<α<β< ,∴aβ<1.
,∴aβ<1. ∴1+a(x-β)=1+ax-aβ>1-aβ>0.
∴1+a(x-β)=1+ax-aβ>1-aβ>0.
而α-x>0,∴α-f(x)>0.∴f(x)<α. 故 选A.
选A.
 已知α、β是F(x)=0的两根,∴F(x)=a(x-α)(x-β).
已知α、β是F(x)=0的两根,∴F(x)=a(x-α)(x-β).在x∈(0,α)时,f(x)-x=F(x)=a(x-α)(α-β).
∵a>0,x-α<0,x-β<0,∴F(x)>0.∴f(x)>x.
又a-f(x)=α-[F(x)+x]=α-x-F(x)=α-x-a(x-α)(x-β)=(α-
 x)[1+a(α-β)].
x)[1+a(α-β)].∵0<x<α<β<
 ,∴aβ<1.
,∴aβ<1. ∴1+a(x-β)=1+ax-aβ>1-aβ>0.
∴1+a(x-β)=1+ax-aβ>1-aβ>0.而α-x>0,∴α-f(x)>0.∴f(x)<α. 故
 选A.
选A.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x2+1的图象与直线y=x相切,则
x2+1的图象与直线y=x相切,则 = ( )
= ( )
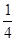

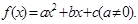 如果
如果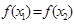 (其中
(其中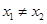 ),则
),则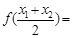 (▲)
(▲)

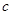

 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
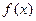 满足:(1)
满足:(1)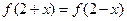 ,(2)被
,(2)被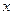 轴截得的弦长为2,(3)在
轴截得的弦长为2,(3)在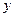 轴截距为6,求此函数解析式。
轴截距为6,求此函数解析式。 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说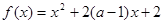 在区间
在区间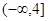 上是减函数,则实数
上是减函数,则实数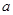 的取值范围是 ( )
的取值范围是 ( )



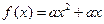 和
和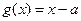 .其中
.其中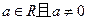 .
. 若函数
若函数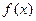 与
与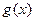 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求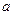 的值;w
的值;w 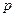 和
和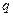 是方程
是方程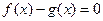 的两根,且满足
的两根,且满足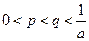 ,
,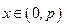 时,
时,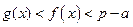 .
.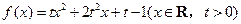 .
. 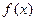 的最小值
的最小值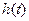 ;
;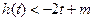 对
对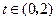 恒成立,求实数
恒成立,求实数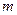 的取值范围.
的取值范围.