题目内容
【题目】某研究公司为了调查公众对某事件的关注程度,在某年的连续6个月内,月份![]() 和关注人数
和关注人数![]() (单位:百)(
(单位:百)(![]() )数据做了初步处理,得到下面的散点图及一些统计量的值.
)数据做了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
17.5 | 35 | 36.5 |
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并建立y关于x的回归方程;
(2)经统计,调查材料费用v(单位:百元)与调查人数满足函数关系![]() ,求材料费用的最小值,并预测此时的调查人数;
,求材料费用的最小值,并预测此时的调查人数;
(3)现从这6个月中,随机抽取3个月份,求关注人数不低于1600人的月份个数![]() 分布列与数学期望.
分布列与数学期望.
参考公式:相关系数 ,若
,若![]() ,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为 ,
,![]() .
.
【答案】(1)![]() (2)1800元,207(3)见解析,1.5
(2)1800元,207(3)见解析,1.5
【解析】
(1)根据散点图,求得![]() ,
,![]() ,再根据提供的数据
,再根据提供的数据![]() ,
,![]() ,求得相关系数
,求得相关系数![]() ,根据
,根据![]() 的大小,说明
的大小,说明![]() 关于
关于![]() 的线性相关程度,是否可用线性回归模型拟合
的线性相关程度,是否可用线性回归模型拟合![]() 与
与![]() 的关系,然后求得
的关系,然后求得![]() ,
,![]() ,
,![]() ,写出回归方程.
,写出回归方程.
(2)根据![]() ,利用基本不等式求解.
,利用基本不等式求解.
(3)![]() 可能的取值为0,1,2,3,分别求得相应的概率,列出分布列,再求期望.
可能的取值为0,1,2,3,分别求得相应的概率,列出分布列,再求期望.
(1)![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴相关系数 ,
,
由于![]() 关于
关于![]() 的相关系数
的相关系数![]() ,
,
这说明![]() 关于
关于![]() 的线性相关程度相当高,可用线性回归模型拟合
的线性相关程度相当高,可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
又 ,且
,且![]() ,
,
∴![]() ,
,
∴回归方程为![]()
(2)![]() ,即调查材料最低成本为1800元,此时
,即调查材料最低成本为1800元,此时![]() ,
,
所以![]() .
.
(3)![]() 可能的取值为0,1,2,3,
可能的取值为0,1,2,3,
且![]() ;
;![]() ;
;![]() ;
;
![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]()

【题目】为了解中学生对交通安全知识的掌握情况,从农村中学和城镇中学各选取100名同学进行交通安全知识竞赛.下图1和图2分别是对农村中学和城镇中学参加竞赛的学生成绩按![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图.
分组,得到的频率分布直方图.
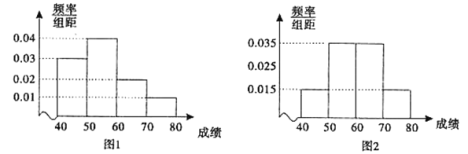
(Ⅰ)分别估算参加这次知识竞赛的农村中学和城镇中学的平均成绩;
(Ⅱ)完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
的把握认为“农村中学和城镇中学的学生对交通安全知识的掌握情况有显著差异”?
成绩小于60分人数 | 成绩不小于60分人数 | 合计 | |
农村中学 | |||
城镇中学 | |||
合计 |
附:![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好