题目内容
12.(1)解关于x的不等式:$\frac{x+2}{k}>1+\frac{x-3}{{k}^{2}}$(k≠0);(2)如果上述不等式的解集为(3,+∞),求k的值.
(3)如果x=3在解集中,求实数k的取值范围.
分析 (1)原不等式可化为(k-1)x>k2-2k-3,分类讨论可得当k=1时解集为R,当k<1且k≠0时解集为{x|x<$\frac{{k}^{2}-2k-3}{k-1}$},当k>1时解集为{x|x>$\frac{{k}^{2}-2k-3}{k-1}$};
(2)由(1)可得k>1且$\frac{{k}^{2}-2k-3}{k-1}$=3,解关于k的方程可得;
(3)可得$\frac{3+2}{k}$>1+$\frac{3-3}{{k}^{2}}$成立,解关于k的不等式可得.
解答 解:(1)不等式$\frac{x+2}{k}>1+\frac{x-3}{{k}^{2}}$可化为k(x+2)>k2+(x-3),
整理可得(k-1)x>k2-2k-3,
当k=1时,不等式的解集为R,
当k<1且k≠0时,不等式的解集为{x|x<$\frac{{k}^{2}-2k-3}{k-1}$},
当k>1时,不等式的解集为{x|x>$\frac{{k}^{2}-2k-3}{k-1}$};
(2)如果上述不等式的解集为(3,+∞),
则k>1且$\frac{{k}^{2}-2k-3}{k-1}$=3,解得k=5;
(3)如果x=3在解集中,则$\frac{3+2}{k}$>1+$\frac{3-3}{{k}^{2}}$成立,
即$\frac{5}{k}$>1,移项通分可得$\frac{k-5}{k}$<0,
解得0<k<5,∴实数k的取值范围为(0,5)
点评 本题考查不等式的解集和方程的解得关系,涉及分类讨论的思想,属中档题.

练习册系列答案
相关题目
8.已知集合A={x|x2-10x+16<0},B={x|0<x<6},则A∩B=( )
| A. | {x|0<x<2} | B. | {x|2<x<6} | C. | {x|6<x<8} |
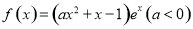 .
.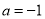 时,函数
时,函数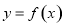 与
与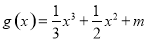 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数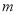 的范围;
的范围;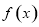 的单调性.
的单调性.