题目内容
17.化简:$\frac{{a}^{\frac{2}{3}}\sqrt{b}}{{a}^{-\frac{1}{2}}\root{3}{b}}$÷$(\frac{{a}^{-1}\sqrt{{b}^{-1}}}{b\sqrt{a}})^{-\frac{2}{3}}$=${a}^{\frac{13}{6}}$${b}^{\frac{7}{6}}$.分析 化为分数指数幂,并利用运算性质即可得出.
解答 解:原式=${a}^{\frac{2}{3}+\frac{1}{2}}$${b}^{\frac{1}{2}-\frac{1}{3}}$×$({a}^{-1-\frac{1}{2}}{b}^{-\frac{1}{2}-1})^{-\frac{2}{3}}$
=${a}^{\frac{7}{6}}{b}^{\frac{1}{6}}$×${a}^{-\frac{3}{2}×(-\frac{2}{3})}$${b}^{-\frac{3}{2}×(-\frac{2}{3})}$
=${a}^{\frac{7}{6}}{b}^{\frac{1}{6}}$×ab
=${a}^{\frac{13}{6}}$${b}^{\frac{7}{6}}$.
故答案为:${a}^{\frac{13}{6}}$${b}^{\frac{7}{6}}$.
点评 本题考查了分数指数幂的运算性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
2.己知f(x)=2sin(x+$\frac{π}{3}$)(x∈R),函数y=f(x+φ)的图象关于直线x=0对称,则φ的值可以是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
7.有下列说法:①-2是16的四次方根;②正数的n次方根有两个;③a的n次方根就是$\root{n}{a}$;④$\root{n}{{a}^{n}}$=a(a≥0),其中正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.已知集合A={x|2x2+3x-2<0},集合B={x|x>a},如果“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围是( )
| A. | a≤-2 | B. | a<-2 | C. | a>-2 | D. | a≥-2 |
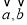 中,若
中,若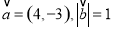 ,且
,且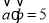 ,则向量
,则向量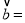 __________.
__________.