题目内容
已知抛物线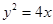 的焦点
的焦点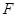 与双曲线
与双曲线 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为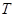 ,且
,且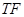 与
与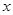 轴垂直,则此双曲线的离心率为( )
轴垂直,则此双曲线的离心率为( )
A.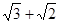 | B.2 | C.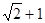  | D.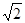 |
C.
解析试题分析:因为抛物线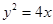 的焦点
的焦点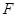 的坐标为
的坐标为 又抛物线
又抛物线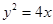 的焦点
的焦点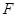 与双曲线
与双曲线 的一个焦点重合,
的一个焦点重合,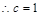 .由已知抛物线
.由已知抛物线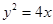 与双曲线
与双曲线 在第一象限内的交点为
在第一象限内的交点为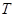 ,且
,且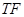 与
与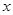 轴垂直,则
轴垂直,则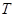 点的横坐标为1,代入
点的横坐标为1,代入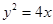 得
得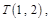 再把
再把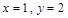 代入
代入 ,与
,与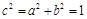 联立得方程组
联立得方程组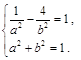 消去
消去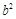 得
得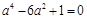 ,解这个关于
,解这个关于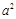 的双二次方程,得
的双二次方程,得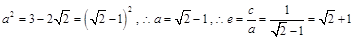 .
.
考点:抛物线与双曲线简单的几何性质(焦点、离心率).

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
抛物线y2=4px(p>0)上一点M到焦点的距离为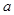 ,则M到y轴距离为 ( )
,则M到y轴距离为 ( )
| A.a-p | B.a+p | C.a-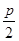 | D.a+2p |
已知F1、F2分别是双曲线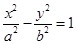 的左、右焦点,P为双曲线右支上的任意一点且
的左、右焦点,P为双曲线右支上的任意一点且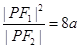 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )
| A.(1,2] | B.[2 +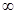 ) ) | C.(1,3] | D.[3,+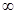 ) ) |
在椭圆 中,
中, 分别是其左右焦点,若椭圆上存在一点P使得
分别是其左右焦点,若椭圆上存在一点P使得 ,则该椭圆离心率的取值范围是( )
,则该椭圆离心率的取值范围是( )
A.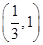 | B.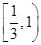 | C.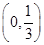 | D. |
若抛物线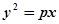 的焦点与椭圆
的焦点与椭圆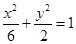 的右焦点重合,则
的右焦点重合,则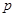 的值为( )
的值为( )
| A.8 | B.2 | C.-4 | D.4 |
已知双曲线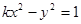 的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )
的一条渐近线与直线2x+y+1=0垂直,则这双曲线的离心率为 ( )
A.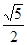 | B.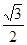 | C.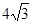 | D.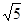 |
椭圆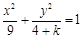 的离心率为
的离心率为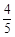 ,则k的值为( )
,则k的值为( )
| A.-21 | B.21 | C.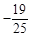 或21 或21 | D.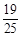 或21 或21 |
已知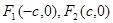 为椭圆
为椭圆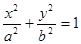 的两个焦点,P为椭圆上
的两个焦点,P为椭圆上 ,则此椭圆离心率的取值范围是 ( )
,则此椭圆离心率的取值范围是 ( )
A. | B. | C.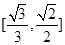 | D.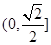 |
 的中心在原点,焦点在坐标轴上,
的中心在原点,焦点在坐标轴上, 是
是 是
是

