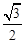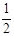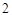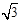题目内容
已知双曲线 的中心在原点,焦点在坐标轴上,
的中心在原点,焦点在坐标轴上, 是
是 上的点,且
上的点,且 是
是 的一条渐近线,则
的一条渐近线,则 的方程为( )
的方程为( )
A. | B. |
C. 或 或 | D. 或 或 |
A
解析试题分析:①当焦点在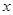 轴上,设方程为
轴上,设方程为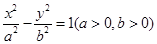 ,
,
由条件有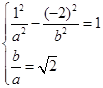 ,解得
,解得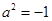 ,不符合题意,所以焦点不可能在
,不符合题意,所以焦点不可能在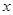 轴上.
轴上.
②①当焦点在 轴上,设方程为
轴上,设方程为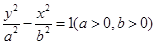 ,
,
由条件有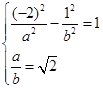 ,解得
,解得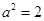 ,
,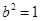 ,其方程为
,其方程为 .
.
故所求满足条件的方程为 ,选A.
,选A.
考点:双曲线方程,渐近线.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
若抛物线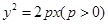 上一点到焦点和抛物线对称轴的距离分别为
上一点到焦点和抛物线对称轴的距离分别为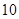 和
和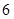 ,则抛物线方程为( )
,则抛物线方程为( )
A.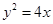 | B.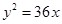 |
C.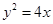 或 或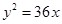 | D.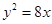 或 或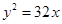 |
已知椭圆E: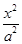 +
+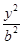 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
A.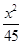 + +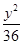 =1 =1 | B.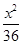 + +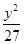 =1 =1 | C.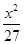 + +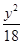 =1 =1 | D. + +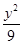 =1 =1 |
与椭圆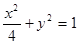 共焦点且过点
共焦点且过点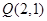 的双曲线方程是( )
的双曲线方程是( )
A.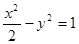 | B.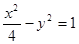 | C.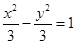 | D.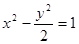 |
已知抛物线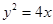 的焦点
的焦点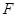 与双曲线
与双曲线 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为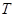 ,且
,且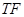 与
与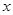 轴垂直,则此双曲线的离心率为( )
轴垂直,则此双曲线的离心率为( )
A.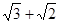 | B.2 | C.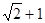  | D.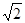 |
双曲线 的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是( )
的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是( )
| A.(-∞,0) | B.(1,+∞) |
| C.(-∞,0)∪(1,+∞) | D.(-∞,-1)∪(1,+∞) |
双曲线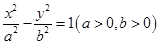 的渐近线方程是2x±y=0,则其离心率为( )
的渐近线方程是2x±y=0,则其离心率为( )
| A.5 | B.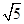 | C.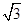 | D.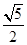 |
已知双曲线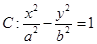
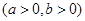 的离心率为
的离心率为 ,则
,则 的渐近线方程为( )
的渐近线方程为( )
A.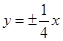 | B.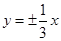 | C.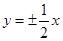 | D.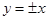 |
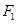 、
、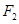 分别为椭圆
分别为椭圆 的两个焦点,点
的两个焦点,点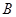 为其短轴的一个端点,若
为其短轴的一个端点,若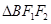 为等边三角形,则该椭圆的离心率为( )
为等边三角形,则该椭圆的离心率为( )