题目内容
【题目】在三棱锥P﹣ABC中.侧梭长均为4.底边AC=4.AB=2,BC=2 ![]() ,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
(Ⅱ)求三棱锥P﹣ABC的体积;
(Ⅲ)求二面角C﹣AD﹣E的余弦值.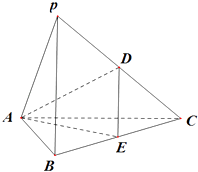
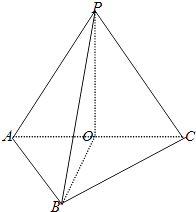
【答案】证明:(Ⅰ)∵PA=PB=PC=AC=4, 取AC的中点O,连接OP,OB,可得:OP⊥AC,![]() ,
,
∵ ![]() ,∴AC2=AB2+BC2 , ∴△ABC为Rt△.
,∴AC2=AB2+BC2 , ∴△ABC为Rt△.
∴OB=OC=2,PB2=OB2+OP2 , ∴OP⊥OB.
又∵AC∩BO=O且AC、OB面ABC,∴OP⊥平面ABC,
又∵OP平面PAC,∴平面PAC⊥平面ABC.)
(Ⅱ)由(I)可知:OP⊥平面ABC,∴OP为三棱锥P﹣ABC的高,且OP= ![]() .
.
直角三角形ABC的面积S= ![]() .
.
∴VP﹣ABC= ![]() =
= ![]() .
.
(Ⅲ)方法一:过点E 作EH⊥AC于H,过点H作HM⊥AD于M,
连接ME,∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,EH⊥AC,EH平面ABC,
∴EH⊥平面PAC,∴ME⊥AD(三垂线定理),
∴∠EMH即为所求的二面角的平面角.
∵E,D分别为中点,EH⊥AC,
∴在RT△HEC中: ![]() ,
, ![]() ,
,
∴ ![]()
在RT△HMA中, ![]() .
.
在RT△HME中, ![]() .
.
∴ 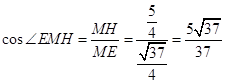 .
.
【解析】(I)利用等腰三角形的性质即可得到OP⊥AC,再利用勾股定理的逆定理即可得到OP⊥OB,利用线面垂直的判定定理即可证明;(II)由(I)可知OP⊥平面ABC,故OP为三棱锥P﹣ABC的高,且OP= ![]() ,直角三角形ABC的面积S=
,直角三角形ABC的面积S= ![]() ,再利用
,再利用 ![]() 即可得出.(III)过点E 作EH⊥AC于H,过点H作HM⊥AD于M,连接ME,由平面PAC⊥平面ABC,EH⊥AC,EH平面ABC,可得EH⊥平面PAC,于是ME⊥AD(三垂线定理),可得∠EMH即为所求的二面角的平面角.利用直角三角形的边角关系求出即可.
即可得出.(III)过点E 作EH⊥AC于H,过点H作HM⊥AD于M,连接ME,由平面PAC⊥平面ABC,EH⊥AC,EH平面ABC,可得EH⊥平面PAC,于是ME⊥AD(三垂线定理),可得∠EMH即为所求的二面角的平面角.利用直角三角形的边角关系求出即可.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

 阅读快车系列答案
阅读快车系列答案