题目内容
(本小题满分16分)定义在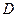 上的函数
上的函数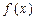 ,如果满足:对任意
,如果满足:对任意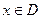 ,存在常数
,存在常数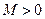 ,都有
,都有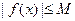 成立,则称
成立,则称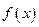 是
是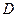 上的有界函数,其中
上的有界函数,其中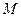 称为函数
称为函数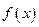 的上界.
的上界.
已知函数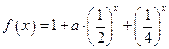 ;
;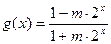 .
.
(1)当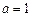 时,求函数
时,求函数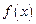 在
在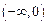 上的值域,并判断函数
上的值域,并判断函数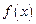 在
在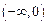 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数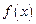 在
在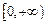 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数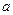 的取值范围;
的取值范围;
(3)若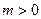 ,函数
,函数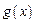 在
在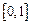 上的上界是
上的上界是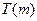 ,求
,求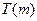 的取值范围.
的取值范围.
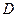 上的函数
上的函数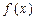 ,如果满足:对任意
,如果满足:对任意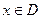 ,存在常数
,存在常数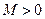 ,都有
,都有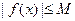 成立,则称
成立,则称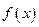 是
是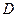 上的有界函数,其中
上的有界函数,其中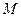 称为函数
称为函数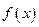 的上界.
的上界.已知函数
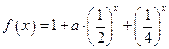 ;
;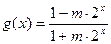 .
. (1)当
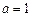 时,求函数
时,求函数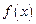 在
在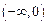 上的值域,并判断函数
上的值域,并判断函数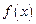 在
在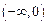 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(2)若函数
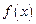 在
在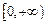 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数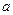 的取值范围;
的取值范围;(3)若
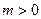 ,函数
,函数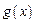 在
在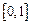 上的上界是
上的上界是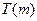 ,求
,求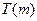 的取值范围.
的取值范围.解:(1)当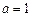 时,
时,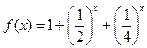
因为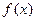 在
在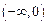 上递减,所以
上递减,所以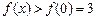 ,即
,即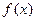 在
在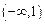 的值域为
的值域为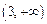 故不存在常数
故不存在常数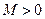 ,使
,使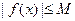 成立
成立
所以函数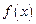 在
在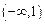 上不是有界函数。 ……………4分
上不是有界函数。 ……………4分
(2)由题意知,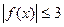 在
在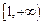 上恒成立。………5分
上恒成立。………5分
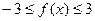 ,
, 
∴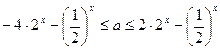 在
在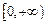 上恒成立………6分
上恒成立………6分
∴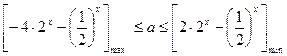 ………7分
………7分
设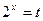 ,
,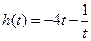 ,
,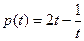 ,由
,由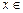
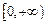 得 t≥1,
得 t≥1,
设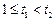 ,
,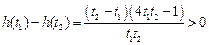
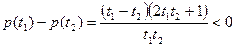
所以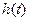 在
在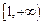 上递减,
上递减,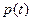 在
在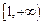 上递增,………9分
上递增,………9分
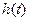 在
在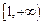 上的最大值为
上的最大值为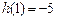 ,
, 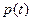 在
在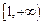 上的最小值为
上的最小值为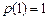
所以实数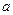 的取值范围为
的取值范围为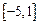 。…………………………………10分
。…………………………………10分
(3)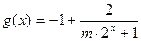 ,
,
∵ m>0 ,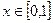 ∴
∴ 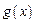 在
在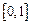 上递减,………12分
上递减,………12分
∴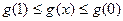 即
即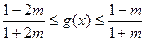 ………13分
………13分
①当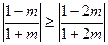 ,即
,即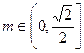 时,
时,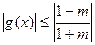 , ………12分
, ………12分
此时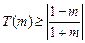 ,………14分
,………14分
②当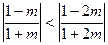 ,即
,即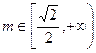 时,
时,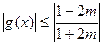 ,
,
此时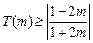 ,
,
综上所述,当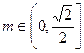 时,
时,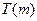 的取值范围是
的取值范围是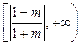 ;
;
当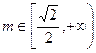 时,
时,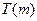 的取值范围是
的取值范围是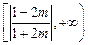 ………16分
………16分
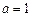 时,
时,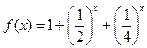
因为
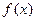 在
在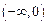 上递减,所以
上递减,所以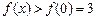 ,即
,即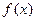 在
在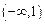 的值域为
的值域为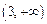 故不存在常数
故不存在常数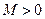 ,使
,使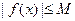 成立
成立所以函数
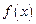 在
在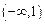 上不是有界函数。 ……………4分
上不是有界函数。 ……………4分(2)由题意知,
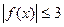 在
在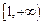 上恒成立。………5分
上恒成立。………5分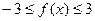 ,
, 
∴
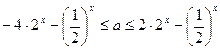 在
在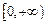 上恒成立………6分
上恒成立………6分∴
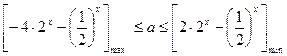 ………7分
………7分设
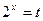 ,
,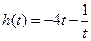 ,
,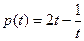 ,由
,由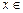
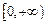 得 t≥1,
得 t≥1,设
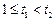 ,
,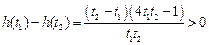
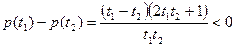
所以
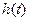 在
在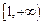 上递减,
上递减,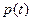 在
在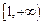 上递增,………9分
上递增,………9分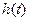 在
在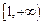 上的最大值为
上的最大值为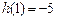 ,
, 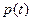 在
在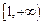 上的最小值为
上的最小值为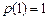
所以实数
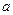 的取值范围为
的取值范围为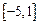 。…………………………………10分
。…………………………………10分(3)
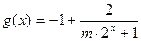 ,
,∵ m>0 ,
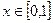 ∴
∴ 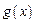 在
在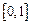 上递减,………12分
上递减,………12分∴
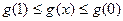 即
即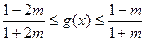 ………13分
………13分①当
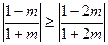 ,即
,即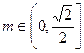 时,
时,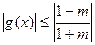 , ………12分
, ………12分此时
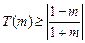 ,………14分
,………14分②当
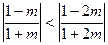 ,即
,即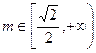 时,
时,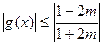 ,
,此时
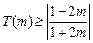 ,
, 综上所述,当
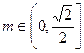 时,
时,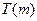 的取值范围是
的取值范围是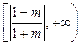 ;
;当
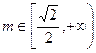 时,
时,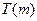 的取值范围是
的取值范围是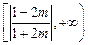 ………16分
………16分略

练习册系列答案
相关题目
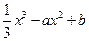 在x=-2处有极值.
在x=-2处有极值. 若对于任意
若对于任意 都有
都有 成立, 求实数
成立, 求实数 的取值范围.
的取值范围.
 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称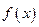 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在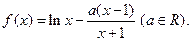
 数
数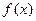 在其定义域内是增函数,求
在其定义域内是增函数,求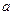 的取值范围;
的取值范围;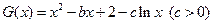 ,方程
,方程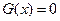 有两根
有两根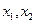 ,记
,记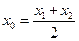 .试探究
.试探究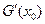 值的符号,其中
值的符号,其中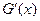 是
是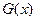 的导函数.
的导函数. ,
, ,
,
 在
在 处取得最大值,求
处取得最大值,求 的范围
的范围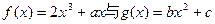 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处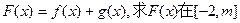 上的最小值。
上的最小值。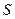 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为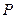 元,
元,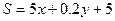 ,
,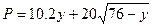 ;其中
;其中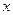 为每吨煤的价格(单位:元),
为每吨煤的价格(单位:元),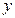 为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.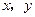 满足
满足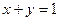 ,,则
,,则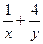 的最小值为______________
的最小值为______________