Question

求证：正△ABC外接圆上的任意一点P到三角形三个顶点的距离的平方和为定值．

Answer 1

考点：两点间距离公式的应用

专题：直线与圆

分析：以正三角形的中心O为坐标原点，BC的中垂线为y轴建立坐标系，设外接圆的半径为R，可得点的坐标和圆的方程，由两点间的距离可得三个距离的平方，相加可得结论．

解答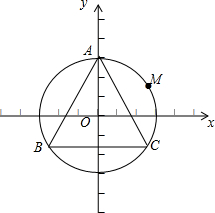： 证明：以正三角形的中心（外接圆的圆心）O为坐标原点，BC的中垂线为y轴建立坐标系，
设外接圆的半径为R，可得A（0，R），B（-

3 R

2

，-

R

2

），C（

3 R

2

，-

R

2

），
则外接圆的方程为x²+y²=R²，故可设圆上的动点M（Rcosθ，Rsinθ），
由两点间的距离公式可得|MA|²=（Rcosθ）²+（Rsinθ-R）²=2R²（1-sinθ），
|MB|²=（Rcosθ+

3 R

2

）²+（Rsinθ+

R

2

）²=R²（2+

3

cosθ+sinθ），
|MC|²=（Rcosθ-

3 R

2

）²+（Rsinθ+

R

2

）²=R²（2-

3

cosθ+sinθ），
以上3式相加可得|MA|²+|MB|²+|MC|²=R²（2-2sinθ+2+

3

cosθ+sinθ+2-

3

cosθ+sinθ）=6R²，为定值．

点评：本题考查两点间的距离公式，建系是解决问题的关键，属基础题．