题目内容
已知函数f(x)=(mx+1)(lnx-1).
(1)若m=1,求曲线y=f(x)在x=1的切线方程;
(2)若函数f(x)在(0,+∞)上是增函数,求实数m的取值范围.
(1)若m=1,求曲线y=f(x)在x=1的切线方程;
(2)若函数f(x)在(0,+∞)上是增函数,求实数m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)若m=1,求出函数的导数即可求曲线y=f(x)在x=1的切线方程;
(2)若函数f(x)在(0,+∞)上是增函数,转化为f′(x)≥0恒成立即可求实数m的取值范围.
(2)若函数f(x)在(0,+∞)上是增函数,转化为f′(x)≥0恒成立即可求实数m的取值范围.
解答:
解:(1)若m=1,则f(x)=(x+1)(lnx-1),
则f(1)=-2,即切点坐标为(1,-2),
函数的f(x)的导数f′(x)=lnx+
,
则f′(1)=1,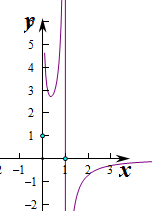
则曲线y=f(x)在x=1的切线方程为y+2=x-1,即y=x-3;
(2)若函数f(x)在(0,+∞)上是增函数,
则f′(x)≥0恒成立,
即f′(x)=m(lnx-1)+m+
≥0恒成立,
则mlnx≥-
,
若x=1,则不等式成立,
若lnx>0,即x>1时,不等式等价为m≥
成立,
设g(x)=
,则g′(x)=
>0,则函数g(x)单调递增,且g(x)<0,此时m≥0,
若lnx<0,即0<x<1时,不等式等价为m≤
成立,
设g(x)=
,则g′(x)=
,
由g′(x)>0解得1+lnx>0,即lnx>-1,
<x<1,此时函数g(x)单调递增,
由g′(x)<0解得1+lnx<0,即lnx<-1,0<x<
,此时函数g(x)单调递减,
故当x=
时,函数g(x)取得极小值为g(
)=
=e,则此时m≤e,
综上0≤m≤e,
即实数m的取值范围是[0,e]
则f(1)=-2,即切点坐标为(1,-2),
函数的f(x)的导数f′(x)=lnx+
| 1 |
| x |
则f′(1)=1,

则曲线y=f(x)在x=1的切线方程为y+2=x-1,即y=x-3;
(2)若函数f(x)在(0,+∞)上是增函数,
则f′(x)≥0恒成立,
即f′(x)=m(lnx-1)+m+
| 1 |
| x |
则mlnx≥-
| 1 |
| x |
若x=1,则不等式成立,
若lnx>0,即x>1时,不等式等价为m≥
| -1 |
| xlnx |
设g(x)=
| -1 |
| xlnx |
| 1+lnx |
| (xlnx)2 |
若lnx<0,即0<x<1时,不等式等价为m≤
| -1 |
| xlnx |
设g(x)=
| -1 |
| xlnx |
| 1+lnx |
| (xlnx)2 |
由g′(x)>0解得1+lnx>0,即lnx>-1,
| 1 |
| e |
由g′(x)<0解得1+lnx<0,即lnx<-1,0<x<
| 1 |
| e |
故当x=
| 1 |
| e |
| 1 |
| e |
| -1 | ||||
|
综上0≤m≤e,
即实数m的取值范围是[0,e]
点评:本题主要考查函数的切线的求解以及函数单调性和导数之间的关系,综合考查导数的应用.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
给出以下四个命题:
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
| A、①为假命题 |
| B、②的否命题为真 |
| C、③的逆否命题为假 |
| D、④的逆命题为真 |
若函数f(x)=-sin2ωx-6sinωxcosωx+3cos2ωx(ω>0)的最小正周期为2π,若对任意x∈R都有f(x)-1≤|f(α)-1|,则tanα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
对两条不相交的空间直线a与b,必存在平面α,使得( )
| A、a?α,b?α |
| B、a?α,b∥α |
| C、a⊥α,b⊥α |
| D、a?α,b⊥α |
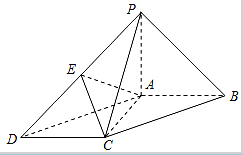 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.