题目内容
抛物线y2=2px三点的纵坐标的平方成等差数列，则这三点的横坐标（ ）
| A、成等差数列 |
| B、成等比数列 |
| C、即成等差数列又成等比数列 |
| D、即不成等差数列又不成等比数列 |
考点：抛物线的简单性质
专题：等差数列与等比数列,圆锥曲线的定义、性质与方程
分析：先设出三点的坐标，根据等差中项的性质，列出关于纵坐标的平方的方程，再由抛物线的方程得到其横坐标也成等差数列．
解答：
解：设三点为A（x1，y1）、B（x2，y2）、C（x3，y3），
因为纵坐标的平方成等差数列，即 y12，y22，y32成等差数列，
所以2y22=y12+y32，
将三点纵坐标分别代入y2=2px得，2（2px2）=2px1+2px2，即2x2=x1+x2，
所以三点横坐标亦成等差数列，
故选：A．
因为纵坐标的平方成等差数列，即 y12，y22，y32成等差数列，
所以2y22=y12+y32，
将三点纵坐标分别代入y2=2px得，2（2px2）=2px1+2px2，即2x2=x1+x2，
所以三点横坐标亦成等差数列，
故选：A．
点评：本题主要考查抛物线的标准方程，以及等差中项的性质，属于基础题．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
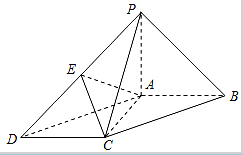如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．