题目内容
在△ABC中,角A、B、C所对的边分别为a,b,c,若(2b-c)cosA=acosC,则A=( )
| A、30° | B、45° |
| C、60° | D、120° |
考点:正弦定理
专题:解三角形
分析:根据正弦定理化简(2b-c)cosA=acosC,利用两角和的正弦公式化简,由内角和的定理、内角的范围求出角A.
解答:
解:由题意得,(2b-c)cosA=acosC,
根据正弦定理得,(2sinB-sinC)cosA=sinAcosC,
2sinBcosA=sinAcosC+cosAsinC,
2sinBcosA=sin(A+C),①
因为A+B+C=180°,所以A+C=180°-B,则sinB=sin(A+C),
代入①得,cosA=
,
由0°<A<180°得,A=60°,
故选:C.
根据正弦定理得,(2sinB-sinC)cosA=sinAcosC,
2sinBcosA=sinAcosC+cosAsinC,
2sinBcosA=sin(A+C),①
因为A+B+C=180°,所以A+C=180°-B,则sinB=sin(A+C),
代入①得,cosA=
| 1 |
| 2 |
由0°<A<180°得,A=60°,
故选:C.
点评:本题考查正弦定理,两角和的正弦公式,以及内角和的定理、内角的范围,熟练掌握定理和公式是解题的关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、已知命题p为“?x∈[0,+∞),(log32)x≤1”,则¬p是真命题 |
| B、若p∨q为假命题,则p、q均为假命题 |
| C、x>2是x>1充分不必要条件 |
| D、“全等三角形的面积相等”的否命题是假命题 |
若函数f(x)=-sin2ωx-6sinωxcosωx+3cos2ωx(ω>0)的最小正周期为2π,若对任意x∈R都有f(x)-1≤|f(α)-1|,则tanα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
命题“若x2<1,则-1<x<1”的逆否命题是( )
| A、若x2≥1,则x≥1且x≤-1 |
| B、若-1<x<1,则x2<1 |
| C、若x>1或x<-1,则x2>1 |
| D、若x≥1或x≤-1,则x2≥1 |
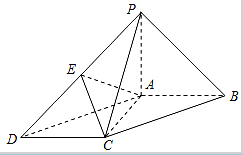 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.