题目内容
已知侧棱垂直于底面的四棱柱,ABCD-A1B1C1D1的底面是菱形,且AD="A" A1,
点F为棱BB1的中点,点M为线段AC1的中点.
(1)求证: MF∥平面ABCD
(2)求证:平面AFC1⊥平面ACC1A1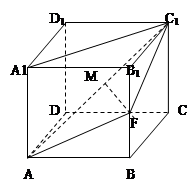
(1)证明见解析;(2)证明见解析.
解析试题分析:
解题思路:(1)构造三角形,利用中位线证明线线平行,再利用线面平行的判定定理证明线面平行;
(2)由线面垂直得到线线垂直,再证明线面垂直,进而证明面面垂直.
规律总结:对于空间几何体中的垂直、平行关系的判定,要牢牢记住并灵活进行转化,线线关系是关键.
试题解析:(1)延长C1F交CB的延长线于点N,连接AN.
∵F是BB1的中点,∴F为C!N的中点,B为CN的中点,
∴又因为M为线段AC!的中点,∴MF∥AN,
又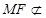 平面ABCD,
平面ABCD,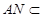 平面ABCD,
平面ABCD,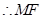 ∥平面ABCD.
∥平面ABCD.
连接BD,由题知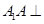 平面AB-CD,又
平面AB-CD,又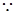
 平面ABCD,
平面ABCD,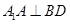 .
.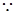 四边形ABCD为菱形,
四边形ABCD为菱形,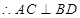 .
.
又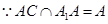 ,
,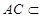 平面
平面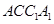 ,
,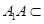 平面
平面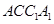 ,
,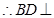 平面
平面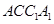 .
.
在四边形DANB中,DA∥BN,且DA=BN,,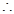 四边形DANB为平行四边形,
四边形DANB为平行四边形,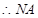 ∥BD,
∥BD,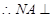 平面
平面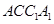 。又
。又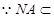 平面
平面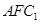 ,
,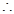 平面
平面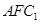 ⊥平面
⊥平面 .
.
考点:1.线面平行的判定定理;2.面面垂直的判定定理.

练习册系列答案
相关题目
 中,
中,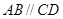 ,
,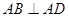 ,且
,且 .现以
.现以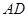 为一边向形外作正方形
为一边向形外作正方形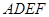 ,然后沿边
,然后沿边 为
为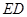 的中点,如图2.
的中点,如图2.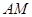 ∥平面
∥平面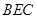 ;
;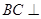 平面
平面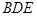 ;
; 到平面
到平面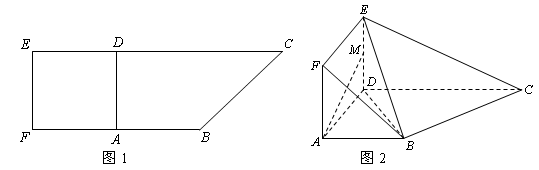
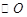 的直径AB=3,点C为
的直径AB=3,点C为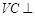 平面ABC,且VC=2,点M为线段VB的中点.
平面ABC,且VC=2,点M为线段VB的中点.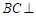 平面VAC;
平面VAC;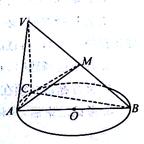
 中,
中, 、
、 分别为
分别为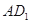 ,
, 中点。
中点。 与
与 所成角的大小;
所成角的大小; 平面
平面 。
。
 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为 .点
.点 分别是棱
分别是棱 上共面的四点,平面
上共面的四点,平面 平面
平面 ,
, 平面
平面 .
.
 ,求四边形
,求四边形
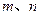 是不同的直线,
是不同的直线,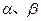 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题: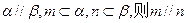
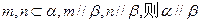
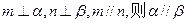
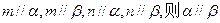
 是两条不同的直线,
是两条不同的直线,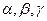 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: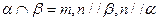 ,则
,则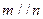 ;
;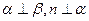 ,则
,则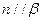 ;
;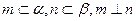 ,则
,则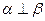 ;
;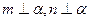 ,则
,则