题目内容
在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,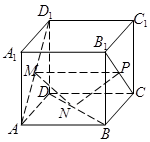
求证:(1)MN∥平面CC1D1D. (2)平面MNP∥平面CC1D1D.
(1)见解析(2)见解析
解析试题分析:
(1)连接AC,CD1 N为BD中点, N为AC中点,又 因为M为AD1中点,
N为AC中点,又 因为M为AD1中点, MN//CD1
MN//CD1 MN//平面CC1D1D
MN//平面CC1D1D
(2)连接BC1,C1D,B1BCC1为正方形,P为B1C中点, P为BC1中点,N为BD中点,
P为BC1中点,N为BD中点, PN// C1D
PN// C1D  PN//平面CC1D1D,
PN//平面CC1D1D,
且MN∩PN=N 平面MNP∥平面CC1D1D.
平面MNP∥平面CC1D1D.
试题解析:
证明:(1)连接AC,CD1,
因为ABCD为正方形,N为BD中点,
所以N为AC中点,
又 因为M为AD1中点,
所以MN//CD1
因为MN¢平面CC1D1D, CD1 平面CC1D1D,
平面CC1D1D,
所以MN//平面CC1D1D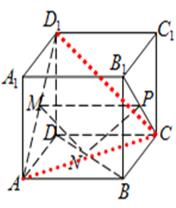
(2)连接BC1,C1D,
因为B1BCC1为正方形,P为B1C中点,
所以P为BC1中点,
又 因为N为BD中点,
所以PN// C1D
因为PN¢平面CC1D1D, CD1 平面CC1D1D,
平面CC1D1D,
所以PN//平面CC1D1D
由(1)知 MN//平面CC1D1D且MN∩PN=N
所以平面MNP∥平面CC1D1D.
考点:线面平行,面面平行.

练习册系列答案
相关题目
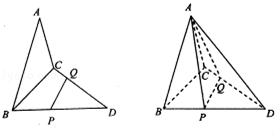
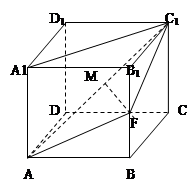
 中,
中,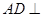 平面
平面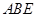 ,
,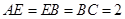 ,
, 为
为 上的点,
上的点, 平面
平面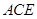
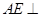 平面
平面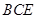 ;
;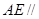 平面
平面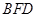 ;
;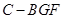 的体积。
的体积。
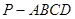 的底面为菱形,
的底面为菱形,
 面
面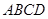 ,且
,且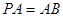 ,
,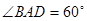 ,
,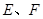 分别是
分别是 的中点.
的中点.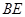 ∥平面
∥平面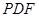 ;
;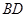 作一平面交棱
作一平面交棱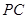 于点
于点 ,若二面角
,若二面角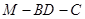 的大小为
的大小为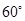 ,求
,求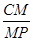 的值.
的值.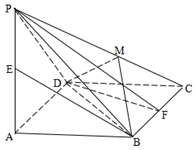
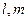 表示直线,
表示直线,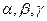 表示平面):
表示平面):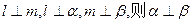 ;② 若
;② 若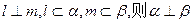 ;
;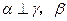 ∥
∥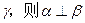 ;④ 若
;④ 若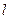 ∥
∥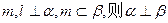 .
.
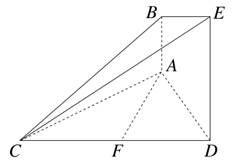
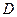 为
为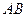 的中点,
的中点,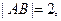
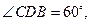
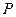 为
为 内的动点,且
内的动点,且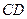 的距离为
的距离为 则
则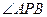 的最大值为________________.
的最大值为________________.