题目内容
如图1,在直角梯形 中,
中,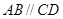 ,
,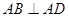 ,且
,且 .现以
.现以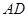 为一边向形外作正方形
为一边向形外作正方形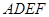 ,然后沿边
,然后沿边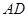 将正方形
将正方形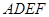 翻折,使平面
翻折,使平面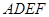 与平面
与平面 垂直,
垂直, 为
为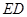 的中点,如图2.
的中点,如图2.
(1)求证: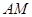 ∥平面
∥平面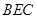 ;
;
(2)求证: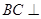 平面
平面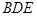 ;
;
(3)求点 到平面
到平面 的距离.
的距离.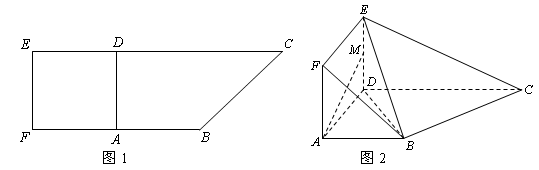
(1)见解析(2)见解析(3)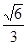
解析试题分析:(1)取EC的中点为N,则MN平行且等于CD的一半,由AB平行且等于CD的一半及平行公理知,NM平行且等于AB,所以ABNM是平行四边形,所以AM平行BN,所以AM平行面BEC;(2)由面ADEF⊥面ADCB及DE⊥AD,面面垂直性质定理知,DE⊥面ADCB,所以AD⊥BC,通过计算及勾股定理可知DB⊥BC,由线面垂直的判定定理可得BC垂直面DBE;(3)先算出三棱锥E-DBC的体积及三角形EBC的面积,再利用三棱锥E-DCB的体积与三棱锥D-EBC的体积相等即可求出点D到面BEC的距离.
试题解析:(1)证明:取 中点
中点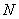 ,连结
,连结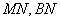 .
.
在△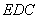 中,
中,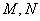 分别为
分别为 的中点,
的中点,
所以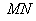 ∥
∥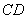 ,且
,且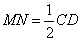 .
.
由已知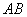 ∥
∥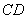 ,
,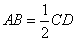 ,
,
所以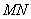 ∥
∥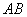 ,且
,且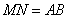 . 3分
. 3分
所以四边形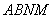 为平行四边形.
为平行四边形.
所以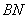 ∥
∥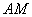 . 4分
. 4分
又因为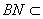 平面
平面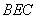 ,且
,且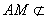 平面
平面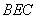 ,
,
所以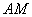 ∥平面
∥平面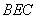 . 4分
. 4分
(2)证明:在正方形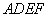 中,
中,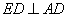 .
.
又因为平面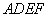
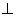 平面
平面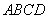 ,且平面
,且平面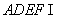 平面
平面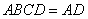 ,
,
所以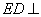 平面
平面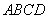 .
.
所以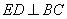 . 6分
. 6分
在直角梯形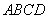 中,
中,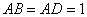 ,
,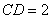 ,可得
,可得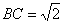 .
.
在△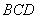 中,
中,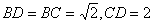 ,
, 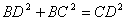 .
.
所以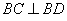 .
.

练习册系列答案
相关题目
 中,四边形
中,四边形 是正方形,
是正方形, ,
, ,
, 分别为
分别为 的中点.
的中点. 平面
平面 ;
; 的平面角的大小.
的平面角的大小.
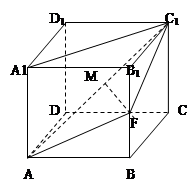
 中,平面
中,平面 侧面
侧面 ,且
,且
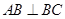 ;
;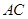 与平面
与平面 所成的角为
所成的角为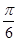 ,求锐二面角
,求锐二面角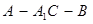 的大小。
的大小。
 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
 与
与 所成角的大小;
所成角的大小; 与平面
与平面 所成角的正弦值.
所成角的正弦值.  中,
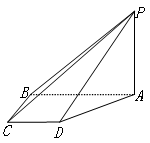
中, ⊥底面
⊥底面 ,四边形
,四边形 ⊥
⊥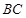 ,
,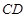 ,
,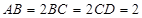 ,
,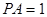 .
.
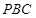 ⊥平面
⊥平面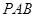 ;
;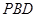 的距离;
的距离;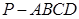 中,底面
中,底面 为矩形,
为矩形, 平面
平面 是
是 的中点.
的中点. //平面
//平面 ;
; ,三棱锥
,三棱锥 的体积
的体积 ,求
,求 到平面
到平面 的距离.
的距离.
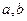 为直线,
为直线,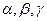 为平面,有下列三个命题:
为平面,有下列三个命题: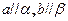 ,则
,则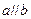 ;
;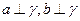 ,则
,则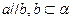 ,则
,则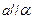 ;
;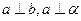 ,则
,则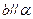 ;
;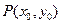 到直线
到直线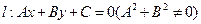 的有向距离为
的有向距离为 .已知点
.已知点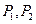 到直线
到直线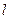 的有向距离分别是
的有向距离分别是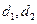 ,给出以下命题:
,给出以下命题: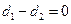 ,则直线
,则直线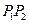 与直线
与直线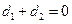 ,则直线
,则直线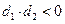 ,则直线
,则直线