题目内容
设 是两条不同的直线,
是两条不同的直线,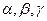 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若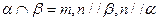 ,则
,则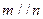 ;
;
②若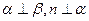 ,则
,则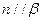 ;
;
③若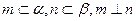 ,则
,则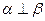 ;
;
④若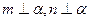 ,则
,则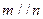 ;
;
其中正确命题有_____________.(填上你认为正确命题的序号)
①④
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设 是两条不同的直线,
是两条不同的直线,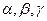 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若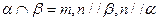 ,则
,则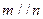 ;
;
②若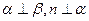 ,则
,则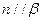 ;
;
③若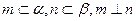 ,则
,则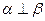 ;
;
④若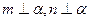 ,则
,则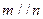 ;
;
其中正确命题有_____________.(填上你认为正确命题的序号)
①④
解析

 阅读快车系列答案
阅读快车系列答案