题目内容
对于定义域为D的函数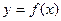 ,若同时满足下列条件:
,若同时满足下列条件:
①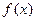 在D内单调递增或单调递减;
在D内单调递增或单调递减;
②存在区间[ ]
]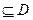 ,使
,使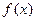 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把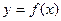 (
(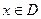 )叫闭函数。
)叫闭函数。
(1)求闭函数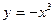 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数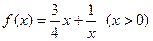 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若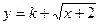 是闭函数,求实数
是闭函数,求实数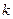 的取值范围。
的取值范围。
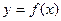 ,若同时满足下列条件:
,若同时满足下列条件:①
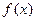 在D内单调递增或单调递减;
在D内单调递增或单调递减;②存在区间[
 ]
]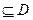 ,使
,使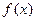 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把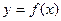 (
(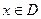 )叫闭函数。
)叫闭函数。(1)求闭函数
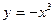 符合条件②的区间[
符合条件②的区间[ ];
];(2)判断函数
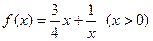 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;(3)若
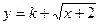 是闭函数,求实数
是闭函数,求实数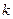 的取值范围。
的取值范围。 (1)所求的区间为[-1,1] (2)函数在定义域内不单调递增或单调递减,从而该函数不是闭函数 (3)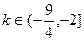
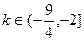
(1)由题意,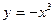 在[
在[ ]上递减,则
]上递减,则 解得
解得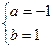
所以,所求的区间为[-1,1]
(2)取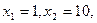 则
则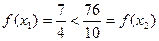 ,即
,即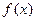 不是
不是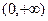 上的减函数。
上的减函数。
取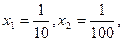
 ,
,
即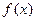 不是
不是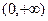 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)若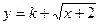 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数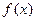 的值域为[
的值域为[ ],即
],即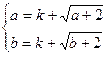 ,
, 为方程
为方程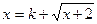 的两个实数根,
的两个实数根,
即方程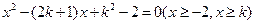 有两个不等的实根。
有两个不等的实根。
当 时,有
时,有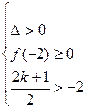 ,解得
,解得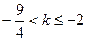 。
。
当 时,有
时,有 ,无解。
,无解。
综上所述,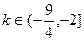 。
。
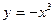 在[
在[ ]上递减,则
]上递减,则 解得
解得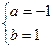
所以,所求的区间为[-1,1]
(2)取
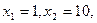 则
则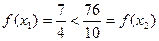 ,即
,即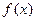 不是
不是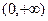 上的减函数。
上的减函数。取
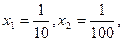
 ,
,即
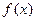 不是
不是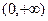 上的增函数
上的增函数所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)若
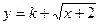 是闭函数,则存在区间[
是闭函数,则存在区间[ ],在区间[
],在区间[ ]上,函数
]上,函数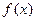 的值域为[
的值域为[ ],即
],即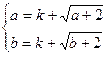 ,
, 为方程
为方程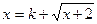 的两个实数根,
的两个实数根,即方程
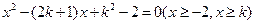 有两个不等的实根。
有两个不等的实根。当
 时,有
时,有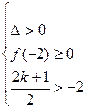 ,解得
,解得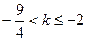 。
。当
 时,有
时,有 ,无解。
,无解。综上所述,
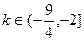 。
。
练习册系列答案
相关题目
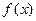 是定义域在
是定义域在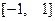 上的奇函数,且其图象上任意两点连线的斜率均小于零.
上的奇函数,且其图象上任意两点连线的斜率均小于零.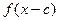 ,
,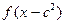 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数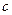 的取值范围;
的取值范围;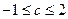 ,则
,则 是
是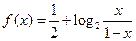 的图象上任意两点,设点
的图象上任意两点,设点 ,且
,且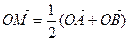 ,若
,若 ,其中
,其中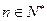 ,且
,且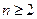 。
。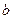 的值;
的值;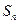 ;
;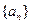 中
中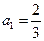 ,当
,当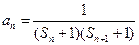 ,设数列
,设数列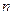 项和为
项和为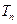 ,
,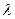 的取值范围使
的取值范围使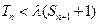 对一切
对一切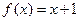 ,设
,设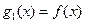 ,
,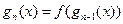
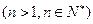
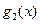 ,
,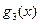 的表达式,并猜想
的表达式,并猜想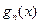
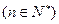 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)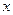 的函数
的函数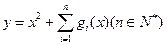 在区间
在区间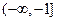 上的最小值为6,求
上的最小值为6,求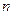 的值
的值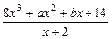 ,定义域为[-1,1]
,定义域为[-1,1]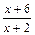 均成立,求实数a,b的值.
均成立,求实数a,b的值. 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?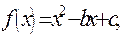 若
若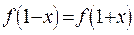 ,且
,且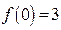 。求
。求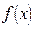
 ,函数
,函数 表示
表示 中的最大者,则
中的最大者,则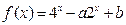 ,当
,当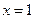 时,
时,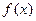 有最小值
有最小值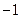 ;
;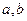 的值; (2)求满足
的值; (2)求满足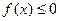 的
的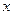 的集合
的集合 ;
;