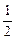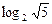题目内容
已知函数f(x)=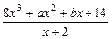 ,定义域为[-1,1]
,定义域为[-1,1]
(Ⅰ)若a=b=0,求f(x)的最小值; (Ⅱ)若对任意x∈[-1,1],不等式6≤f(x)≤5+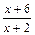 均成立,求实数a,b的值.
均成立,求实数a,b的值.
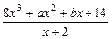 ,定义域为[-1,1]
,定义域为[-1,1](Ⅰ)若a=b=0,求f(x)的最小值; (Ⅱ)若对任意x∈[-1,1],不等式6≤f(x)≤5+
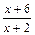 均成立,求实数a,b的值.
均成立,求实数a,b的值.(1)当x=-1或 时,f(x)取到最小值6.
时,f(x)取到最小值6.
(2)a=0,b=0是满足题意的唯一一组值.
 时,f(x)取到最小值6.
时,f(x)取到最小值6. (2)a=0,b=0是满足题意的唯一一组值.
(Ⅰ)当a=b=0时
f(x)=
f′(x)=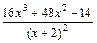
记h(x)=16x3+48x2-14
令h(x)=0,得x=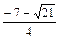 ,x=
,x=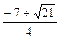 ,或x=
,或x= .
.
若x∈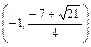 或
或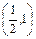 ,则f′(x)>0,即f(x)在
,则f′(x)>0,即f(x)在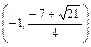 和
和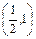 上为增函数.
上为增函数.
若x∈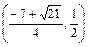 ,则f′(x)<0,即f(x)在
,则f′(x)<0,即f(x)在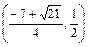 上为减函数,
上为减函数,
∴f( )=6为极小值.
)=6为极小值.
又f(-1)=6,
∴f(x)在[-1,1]上的最小值为f(-1)=f( )=6.
)=6.
∴f(x)≥6,当x=-1或 时,f(x)取到最小值6.
时,f(x)取到最小值6.
(Ⅱ)6≤f(x)≤5+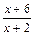
 6≤
6≤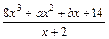 ≤5+
≤5+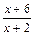
 6(x+2)≤8x3+ax2+6x+14≤6x+16
6(x+2)≤8x3+ax2+6x+14≤6x+16
 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4
即
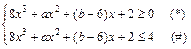
在不等式(*)中,取x=-1, ,得
,得
-8+a-(b-6)+2≥0
1+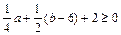
即a-b≥0,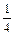 a+
a+ b≥0
b≥0
亦即-a+b≤0 (1)
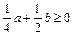 (2)
(2)
在不等式(#)中,取x=1,- ,得
,得
8+a+(b-6)+2≤4
-1+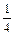 a-
a- (b-6)+2≤4
(b-6)+2≤4
即a+b≤0,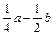 ≤0
≤0
亦即a+b≤0 (3)
-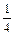 a+
a+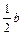 ≥0 (4)
≥0 (4)
(1)+(3),得b≤0
(2)+(4),得b≥0
∴b=0
将b=0代入(2),得a≥0
将b=0代入(3),得a≤0
∴a=0
当a=0,b=0时,
6≤f(x)≤5+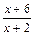
 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4
 0≤8x3-6x+2≤4
0≤8x3-6x+2≤4
记g(x)=8x3-6x+2
 0≤g(x)≤4
0≤g(x)≤4
g′(x)=24x2-6,
令g′(x)=0,得x=- 或x=
或x= .
.
若x∈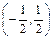 或
或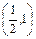 则g′(x)>0,即g(x)在
则g′(x)>0,即g(x)在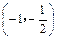 和
和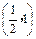 上为增函数.
上为增函数.
若x∈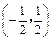 ,则g′(x)<0,即g(x)在
,则g′(x)<0,即g(x)在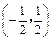 上为减函数,
上为减函数,
∴g(-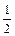 )=4为极大值,g(
)=4为极大值,g(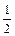 )=0为极小值.
)=0为极小值.
又g(-1)=0,g(1)=4,
∴g(x)在[-1,1]上最大值为g(-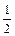 )=g(1)=4,
)=g(1)=4,
g(x)在[-1,1]上最小值为g(-1)=g(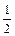 )=0.
)=0.
知0≤g(x)≤4,对一切x∈[-1,1]成立.
综上可知a=0,b=0是满足题意的唯一一组值.
f(x)=

f′(x)=
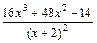
记h(x)=16x3+48x2-14
令h(x)=0,得x=
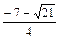 ,x=
,x=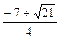 ,或x=
,或x= .
.若x∈
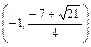 或
或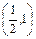 ,则f′(x)>0,即f(x)在
,则f′(x)>0,即f(x)在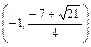 和
和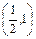 上为增函数.
上为增函数.若x∈
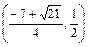 ,则f′(x)<0,即f(x)在
,则f′(x)<0,即f(x)在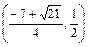 上为减函数,
上为减函数,∴f(
 )=6为极小值.
)=6为极小值.又f(-1)=6,
∴f(x)在[-1,1]上的最小值为f(-1)=f(
 )=6.
)=6.∴f(x)≥6,当x=-1或
 时,f(x)取到最小值6.
时,f(x)取到最小值6.(Ⅱ)6≤f(x)≤5+
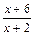
 6≤
6≤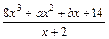 ≤5+
≤5+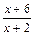
 6(x+2)≤8x3+ax2+6x+14≤6x+16
6(x+2)≤8x3+ax2+6x+14≤6x+16 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4即

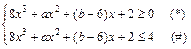
在不等式(*)中,取x=-1,
 ,得
,得-8+a-(b-6)+2≥0
1+
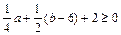
即a-b≥0,
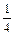 a+
a+ b≥0
b≥0亦即-a+b≤0 (1)
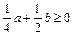 (2)
(2)在不等式(#)中,取x=1,-
 ,得
,得8+a+(b-6)+2≤4
-1+
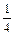 a-
a- (b-6)+2≤4
(b-6)+2≤4即a+b≤0,
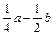 ≤0
≤0亦即a+b≤0 (3)
-
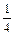 a+
a+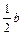 ≥0 (4)
≥0 (4)(1)+(3),得b≤0
(2)+(4),得b≥0
∴b=0
将b=0代入(2),得a≥0
将b=0代入(3),得a≤0
∴a=0
当a=0,b=0时,
6≤f(x)≤5+
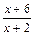
 0≤8x3+ax2+(b-6)x+2≤4
0≤8x3+ax2+(b-6)x+2≤4 0≤8x3-6x+2≤4
0≤8x3-6x+2≤4记g(x)=8x3-6x+2
 0≤g(x)≤4
0≤g(x)≤4g′(x)=24x2-6,
令g′(x)=0,得x=-
 或x=
或x= .
.若x∈
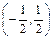 或
或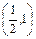 则g′(x)>0,即g(x)在
则g′(x)>0,即g(x)在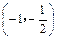 和
和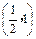 上为增函数.
上为增函数.若x∈
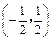 ,则g′(x)<0,即g(x)在
,则g′(x)<0,即g(x)在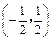 上为减函数,
上为减函数,∴g(-
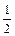 )=4为极大值,g(
)=4为极大值,g(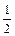 )=0为极小值.
)=0为极小值.又g(-1)=0,g(1)=4,
∴g(x)在[-1,1]上最大值为g(-
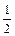 )=g(1)=4,
)=g(1)=4,g(x)在[-1,1]上最小值为g(-1)=g(
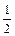 )=0.
)=0.知0≤g(x)≤4,对一切x∈[-1,1]成立.
综上可知a=0,b=0是满足题意的唯一一组值.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
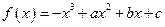 在
在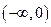 上是减函数,在
上是减函数,在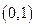 上是增函数,函数
上是增函数,函数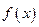 在
在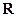 上有三个零点,且1是其中一个零点.
上有三个零点,且1是其中一个零点.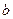 的值;
的值;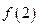 的取值范围;
的取值范围;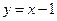 与函数
与函数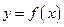 的图像交点个数的情况,并说明理由.
的图像交点个数的情况,并说明理由.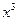 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数. ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f(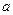
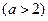 ,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。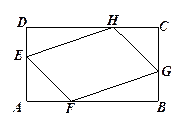
 的图象上任意两点,且
的图象上任意两点,且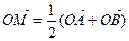 ,已知点M的横坐标为
,已知点M的横坐标为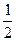 .
.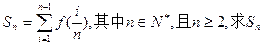 ;
;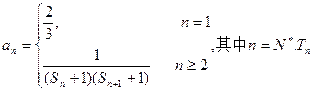 为数列
为数列 的前n项和,若
的前n项和,若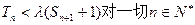 都成立,试求
都成立,试求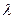 的取值范围.
的取值范围.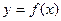 ,若同时满足下列条件:
,若同时满足下列条件: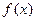 在D内单调递增或单调递减;
在D内单调递增或单调递减; ]
]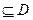 ,使
,使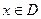 )叫闭函数。
)叫闭函数。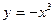 符合条件②的区间[
符合条件②的区间[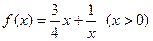 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;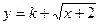 是闭函数,求实数
是闭函数,求实数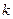 的取值范围。
的取值范围。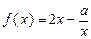
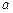
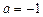 时,求函数
时,求函数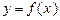 的值域;
的值域;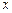 的值
的值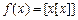 ,其中
,其中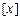 表示不超过x的最大整数,如:
表示不超过x的最大整数,如: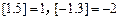 ,当
,当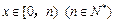 时,设函数
时,设函数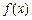 的值域为A,记集合A中的元素个数为an,则式子
的值域为A,记集合A中的元素个数为an,则式子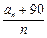 的最小值为( )
的最小值为( )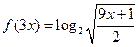 ,则
,则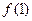 的值为( )
的值为( )