题目内容
已知 是关于
是关于 的方程
的方程 的两个根.
的两个根.
(1)求 的值;
的值;
(2)求 的值.
的值.
(1) ;(2)
;(2)  .
.
解析试题分析:先利用一元二次方程根的判别式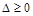 ,得
,得 或
或 ,结合已知条件、韦达定理及平方关系
,结合已知条件、韦达定理及平方关系 ,可得
,可得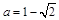 ,从而由韦达定理得
,从而由韦达定理得
(1) 利用诱导公式将欲求式化简,得 ,代入即可求其值;
,代入即可求其值;
(2) 利用诱导公式三角函数基本关系式将欲求式化简成: 代入即可求其值.
代入即可求其值.
试题解析:由已知原方程判别式Δ≥0,即 或
或 ,又
,又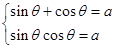
∴(sin θ+cos θ)2=1+2sin θcos θ,即a2-2a-1=0.
∴a=1-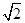 或a=1+
或a=1+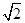 (舍去).∴sin θ+cos θ=sin θcos θ=1-
(舍去).∴sin θ+cos θ=sin θcos θ=1-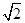 .
.
(1) ="-(sin" θ+cos θ)=
="-(sin" θ+cos θ)=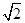 -1
-1
(2)tan(π-θ)-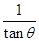 =-tan θ-
=-tan θ-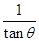
=-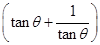 =-
=-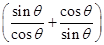 =-
=- =-
=- =
=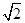 +1.
+1.
考点:1.韦达定理;2.三角函数求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的最小正周期和最大值;
的最小正周期和最大值; 上的单调递减区间.
上的单调递减区间.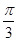 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
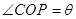 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值. ,
,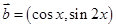 ,
, .
.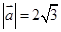 ,求
,求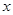 的值;
的值;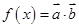 ,求
,求 的最大、最小值.
的最大、最小值. 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示
图象如图所示
 的表达式;
的表达式; 的解;
的解; 的值,使得
的值,使得 在
在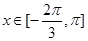 上恒成立;若存在,求出
上恒成立;若存在,求出 为偶函数,周期为2
为偶函数,周期为2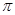 .
.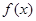 的解析式;
的解析式; 的值.
的值. ,的部分图象如图所示.
,的部分图象如图所示.
 的解析式;
的解析式;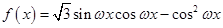 ,其中
,其中 为使
为使 能在
能在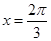 时取得最大值的最小正整数.
时取得最大值的最小正整数. 的三边长
的三边长 、
、 、
、 满足
满足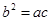 ,且边
,且边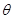 的取值集合为
的取值集合为 ,当
,当 时,求
时,求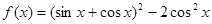
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;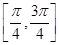 上的值域.
上的值域.