题目内容
定义在区间 上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示
图象如图所示
(Ⅰ)求函数 在
在 的表达式;
的表达式;
(Ⅱ)求方程 的解;
的解;
(Ⅲ)是否存在常数 的值,使得
的值,使得 在
在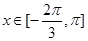 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由
(Ⅰ)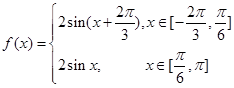 ;(Ⅱ)
;(Ⅱ)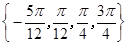 ;(Ⅲ)
;(Ⅲ)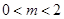
解析试题分析:(Ⅰ)由函数的图像可分两段求解:当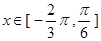 ,
,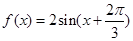 ;当
;当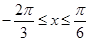 ,
,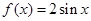 注意运用图像的对称性 故
注意运用图像的对称性 故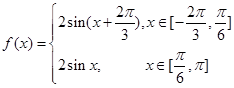 ;(Ⅱ)结合(Ⅰ)中的解析式,分两种情况求出三角方程的解即可;(Ⅲ)先假设存在,然后找出使得
;(Ⅱ)结合(Ⅰ)中的解析式,分两种情况求出三角方程的解即可;(Ⅲ)先假设存在,然后找出使得 在
在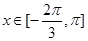 上恒成立的条件,由图像可得
上恒成立的条件,由图像可得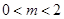
试题解析:(Ⅰ)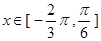 ,
,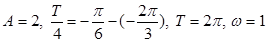
且 过
过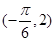 ,∵
,∵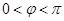 ∴
∴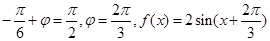
当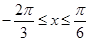 时
时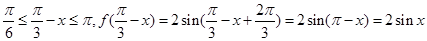 3分
3分
而函数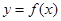 的图象关于直线
的图象关于直线 对称,则
对称,则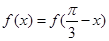 即
即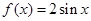 ,
,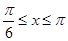
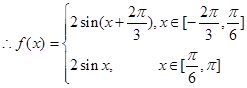 5分
5分
(Ⅱ)当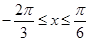 时,
时,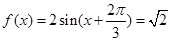
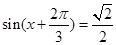
∴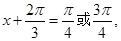 即
即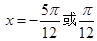
当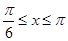 时,
时, ∴
∴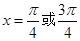
∴方程 的解集是
的解集是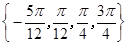 8分
8分
(Ⅲ)存在 假设存在,由条件得: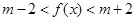 在
在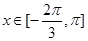 上恒成立
上恒成立
即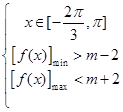 ,由图象可得:
,由图象可得: ∴
∴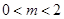 12分
12分
考点:1 利用函数图像求函数解析式;2 解三角方程;3 利用函数图像处理函数不等式的恒成立问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数
 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像.
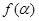 ;
;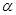 是第三象限角,且
是第三象限角,且 ,求
,求
 时,求
时,求 的最大值及相应的x值;
的最大值及相应的x值; 的图象经过怎样的变换得到f(x)的图象.
的图象经过怎样的变换得到f(x)的图象.  ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
 ,求
,求 面积的最大值及此时
面积的最大值及此时 的值.
的值. 是关于
是关于 的方程
的方程 的两个根.
的两个根. 的值;
的值; 的值.
的值. ,
, .
. ;
; ,求c和ΔABC的面积.
,求c和ΔABC的面积. ,
, .
. 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角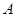 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
, 且
且 ,求
,求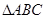 中,角
中,角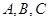 的对边分别为
的对边分别为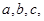 向量
向量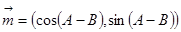 ,
,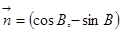 ,且
,且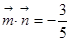 .
.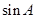 的值;
的值;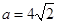 ,
,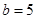 ,求角
,求角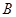 的大小及向量
的大小及向量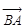 在
在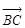 方向上的投影.
方向上的投影.