题目内容
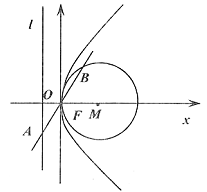
(本题满分14分)如图,已知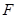 为椭圆
为椭圆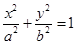
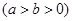 的右焦点,直线
的右焦点,直线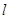 过点
过点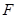 且与双曲线
且与双曲线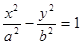 的两条渐进线
的两条渐进线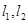 分别交于点
分别交于点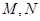 ,与椭圆交于点
,与椭圆交于点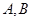 .
.
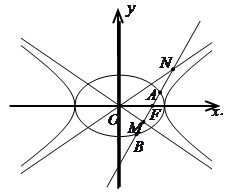
(I)若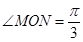 ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。
(II)若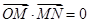 (
(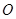 为坐标原点),
为坐标原点),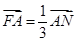 ,求椭圆的离心率
,求椭圆的离心率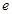
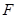 为椭圆
为椭圆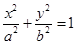
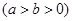 的右焦点,直线
的右焦点,直线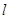 过点
过点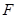 且与双曲线
且与双曲线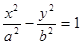 的两条渐进线
的两条渐进线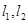 分别交于点
分别交于点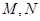 ,与椭圆交于点
,与椭圆交于点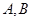 .
.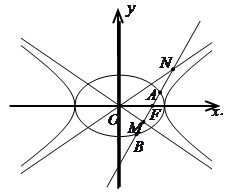
(I)若
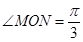 ,双曲线的焦距为4。求椭圆方程。
,双曲线的焦距为4。求椭圆方程。(II)若
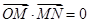 (
(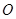 为坐标原点),
为坐标原点),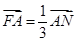 ,求椭圆的离心率
,求椭圆的离心率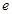
19、(本小题满分14分)
解:(I)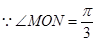 ,
,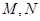 是直线
是直线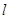 与双曲线两条渐近线的交点,
与双曲线两条渐近线的交点,
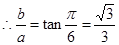 , 即
, 即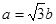 ………………2分
………………2分
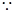 双曲线的焦距为4,
双曲线的焦距为4,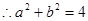 ……………………4分
……………………4分
解得,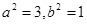
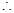 椭圆方程为
椭圆方程为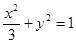 …………5分
…………5分
(II)解:设椭圆的焦距为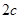 ,则点
,则点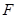 的坐标为
的坐标为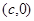
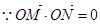 ,
, 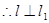
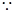 直线
直线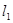 的斜率为
的斜率为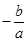 ,
,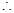 直线
直线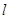 的斜率为
的斜率为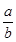 ,
,
 直线
直线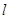 的方程为
的方程为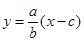 …………………………………………7分
…………………………………………7分
由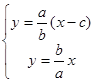 解得
解得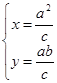 即点
即点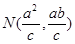
设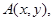 由
由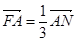 ,得
,得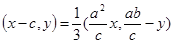
即
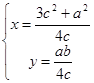
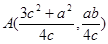 ……10分。
……10分。
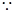 点
点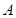 在椭圆上,
在椭圆上,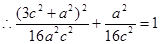 ………………………………12分
………………………………12分
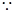
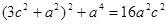 ,
,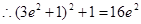
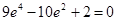
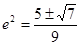
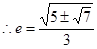
椭圆的离心率是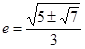 。 -----------------------------------14分
。 -----------------------------------14分
解:(I)
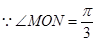 ,
,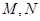 是直线
是直线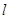 与双曲线两条渐近线的交点,
与双曲线两条渐近线的交点,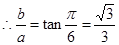 , 即
, 即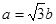 ………………2分
………………2分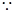 双曲线的焦距为4,
双曲线的焦距为4,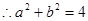 ……………………4分
……………………4分解得,
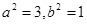
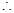 椭圆方程为
椭圆方程为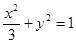 …………5分
…………5分(II)解:设椭圆的焦距为
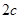 ,则点
,则点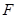 的坐标为
的坐标为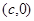
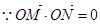 ,
, 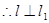
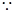 直线
直线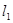 的斜率为
的斜率为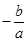 ,
,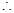 直线
直线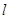 的斜率为
的斜率为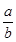 ,
,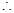 直线
直线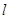 的方程为
的方程为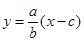 …………………………………………7分
…………………………………………7分由
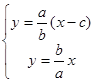 解得
解得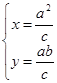 即点
即点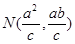
设
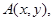 由
由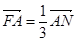 ,得
,得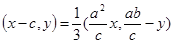
即

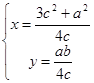
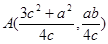 ……10分。
……10分。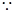 点
点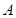 在椭圆上,
在椭圆上,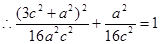 ………………………………12分
………………………………12分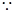
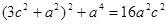 ,
,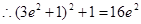
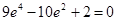
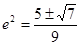
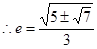
椭圆的离心率是
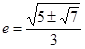 。 -----------------------------------14分
。 -----------------------------------14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
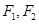 分别为椭圆
分别为椭圆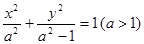 的左、右两个焦点,一条直线
的左、右两个焦点,一条直线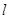 经过点
经过点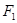 与椭圆交于
与椭圆交于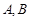 两点, 且
两点, 且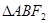 的周长为8。
的周长为8。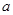 的值;
的值; 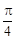 ,求
,求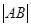 的值。
的值。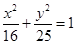 共焦点,且两条准线间的距离为
共焦点,且两条准线间的距离为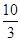 的双曲线方程为( )
的双曲线方程为( )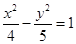 B.
B.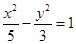 C.
C.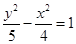 D.
D.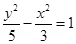
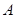 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心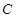 的定点,动点
的定点,动点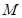 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点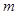 交线段
交线段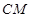 于点
于点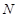 .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系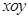 中,设圆
中,设圆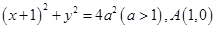 ,记点
,记点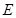 .
.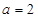 时该椭圆的标准方程;
时该椭圆的标准方程;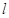 过点
过点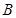 ,点
,点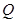 ,若椭圆
,若椭圆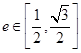 ,求点
,求点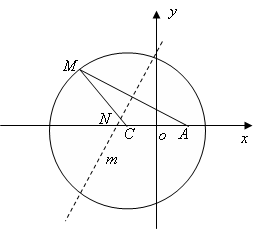
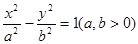 中,
中,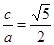 ,且双曲线与椭圆
,且双曲线与椭圆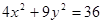 有公共焦点,则双曲线的方程是( )
有公共焦点,则双曲线的方程是( )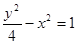
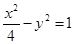
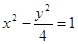
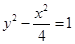
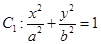 (
(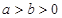 ,且
,且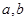 为常数),椭圆
为常数),椭圆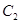 焦点在
焦点在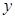 轴上,椭圆
轴上,椭圆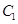 的短轴长相等,且椭圆
的短轴长相等,且椭圆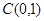 的椭圆
的椭圆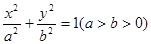 的离心率为
的离心率为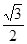 ,椭圆与
,椭圆与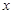 轴交于两点
轴交于两点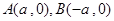 ,过点
,过点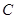 的直线
的直线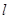 与椭圆交于另一点
与椭圆交于另一点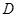 ,并与
,并与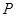 ,直线
,直线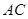 与直线
与直线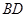 交于点
交于点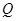
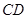 的长;
的长;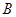 时,求证:
时,求证: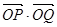 为定值
为定值
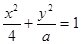 与双曲线
与双曲线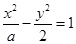 有相同的焦点,则
有相同的焦点,则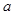 的值是
的值是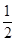
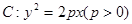 的准线为
的准线为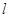 ,焦点为F,
,焦点为F,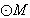 的圆心在
的圆心在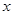 轴的正半轴上,且与
轴的正半轴上,且与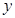 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为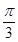 的直线
的直线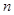 ,交
,交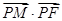 的最小值;
的最小值;