题目内容
15.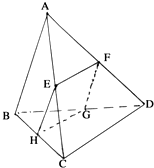 如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.
如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.(1)求证:AB∥平面EFGH;
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
分析 (1)通过证明EH∥平面ABD,得出EH∥AB,从而证明AB∥平面EFGH;
(2)设EH=x,EF=y,由EH∥AB,EF∥CD,求出x、y的关系式,再求四边形EFGH的周长l的取值范围即可.
解答 解:(1)证明:∵四边形EFGH为平行四边形,∴EH∥FG;
∵EH?平面ABD,FG?平面ABD,
∴EH∥平面ABD;
又∵EH?平面ABC,平面ABC∩平面ABD=AB,
∴EH∥AB;
又∵EH?平面EFGH,AB?平面EFGH,
∴AB∥平面EFGH;
(2)设EH=x,EF=y,
∵EH∥AB,EF∥CD,
∴$\frac{EH}{AB}$=$\frac{CE}{CA}$,$\frac{EF}{CD}$=$\frac{AE}{AC}$,
∴$\frac{EH}{AB}$+$\frac{EF}{CD}$=$\frac{CE}{CA}$+$\frac{AE}{AC}$=$\frac{AC}{AC}$=1;
又∵AB=4,CD=6,∴$\frac{x}{4}$+$\frac{y}{6}$=1,
∴y=6(1-$\frac{x}{4}$),且0<x<4;
∴四边形EFGH的周长为
l=2(x+y)=2[x+6(1-$\frac{x}{4}$)]
=12-x,
∴8<12-x<12;
∴四边形EFGH周长的取值范围是(8,12).
点评 本题考查了空间中线面平行的判断与性质的应用问题,也考查了平行线截得线段成比例的应用问题,
是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.函数y=|x|-2cosx的图象大致是( )
| A. | 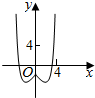 | B. |  | C. | 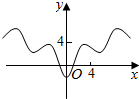 | D. |  |
20.下列说法正确的是( )
| A. | 在△ABC中,A<B是sinA<sinB的充要条件 | |
| B. | $\overrightarrow{a}$$•\overrightarrow{b}$<0 是$\overrightarrow{a}$与$\overrightarrow{b}$夹角为钝角的充要条件 | |
| C. | 若直线a,b,平面α,β满足a⊥α,α⊥β,b?α,b?β则a⊥b能推出b⊥β | |
| D. | 在相关性检验中,当相关性系数r满足|r|>0.632时,才能求回归直线方程 |
7.有专业机构认为甲型H7N9禽流感在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过15人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
| A. | 甲地:总体均值为6,中位数为8 | B. | 乙地:总体均值为5,方差为12 | ||
| C. | 丙地:中位数为5,众数为6 | D. | 丁地:总体均值为3,方差大于0 |
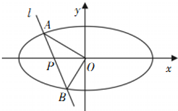 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.