题目内容
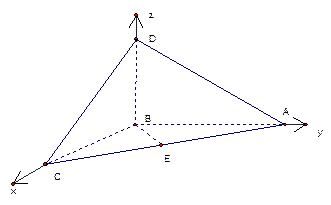
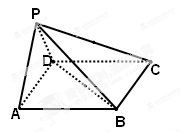
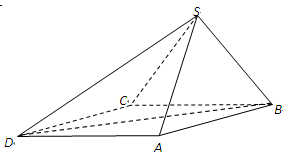
如图,在三棱柱 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱 面
面 ,点
,点 是
是 的中点.
的中点.
(1) 求证: ;(2)求证:
;(2)求证: ∥平面
∥平面

 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱 面
面 ,点
,点 是
是 的中点.
的中点.(1) 求证:
 ;(2)求证:
;(2)求证: ∥平面
∥平面

因为三棱柱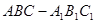 是正三棱柱,所以
是正三棱柱,所以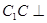 平面
平面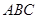 ,
,
又 平面
平面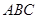 ,所以
,所以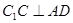 ,……………………………………… 2分
,……………………………………… 2分
又点 是棱
是棱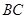 的中点,且
的中点,且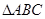 为正三角形,所以
为正三角形,所以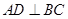 ,
,
因为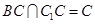 ,所以
,所以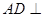 平面
平面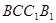 ,………………………………4分
,………………………………4分
又因为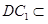 平面
平面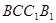 ,所以
,所以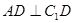 .………………………………6分
.………………………………6分
(2)连接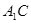 交
交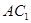 于点
于点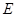 ,再连接
,再连接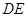 .………7分
.………7分
因为四边形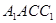 为矩形,
为矩形,
所以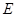 为
为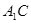 的中点,………………8分
的中点,………………8分
又因为 为
为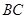 的中点,
的中点,
所以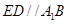 .………………………10分
.………………………10分
又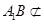 平面
平面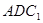 ,
,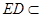 平面
平面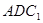 ,
,
所以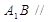 平面
平面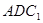 .
.
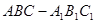 是正三棱柱,所以
是正三棱柱,所以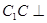 平面
平面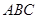 ,
,又
 平面
平面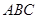 ,所以
,所以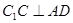 ,……………………………………… 2分
,……………………………………… 2分又点
 是棱
是棱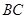 的中点,且
的中点,且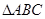 为正三角形,所以
为正三角形,所以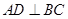 ,
,因为
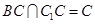 ,所以
,所以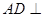 平面
平面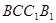 ,………………………………4分
,………………………………4分又因为
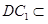 平面
平面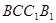 ,所以
,所以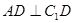 .………………………………6分
.………………………………6分(2)连接
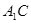 交
交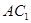 于点
于点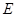 ,再连接
,再连接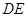 .………7分
.………7分因为四边形
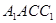 为矩形,
为矩形,所以
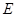 为
为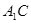 的中点,………………8分
的中点,………………8分又因为
 为
为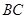 的中点,
的中点,所以
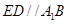 .………………………10分
.………………………10分又
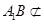 平面
平面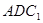 ,
,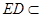 平面
平面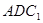 ,
,所以
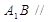 平面
平面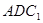 .
.
略

练习册系列答案
相关题目
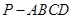 中,底面
中,底面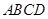 是边长为
是边长为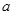 的正方形,侧面
的正方形,侧面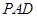
 底面
底面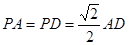 .
.
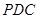 ;
; 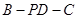 的余弦值.
的余弦值.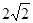 ,SA=SB=
,SA=SB=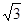 。
。
 中,
中, ,底面
,底面 为直角梯形,
为直角梯形, ,点
,点 在棱
在棱 上,且
上,且 .
. 所成的角;
所成的角; 平面
平面 ;
; 的余弦值.
的余弦值.
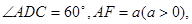 (I)求证:AC⊥BF;
(I)求证:AC⊥BF;
 中,△
中,△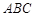 为等腰直角三角形,∠
为等腰直角三角形,∠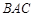 =90°,且
=90°,且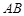 =
=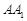 ,
,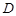 、
、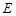 、
、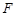 分别为
分别为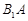 、
、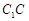 、
、 的中点.
的中点.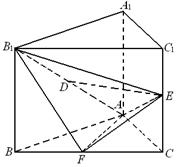
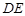 ∥平面
∥平面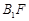 ⊥平面
⊥平面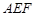 ;
;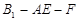 的余弦值
的余弦值 B
B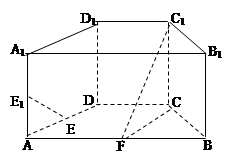
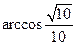 ,求BD的长度.(15分)
,求BD的长度.(15分)