题目内容
20.已知直线过点A(-2,-3)和B(3,0),直线外一点P(-1,2)求过点P与AB垂直的直线.分析 求出直线AB的斜率kAB,利用垂直关系求出直线l的斜率,由点斜式求出直线l的方程.
解答 解:∵直线AB的斜率为
kAB=$\frac{0-(-3)}{3-(-2)}$=$\frac{3}{5}$,
∴与直线AB垂直的直线l的斜率为
kl=-$\frac{5}{3}$,
又直线l过点P(-1,2),
∴直线l的方程为
y-2=-$\frac{5}{3}$(x+1),
化为一般形式为
5x+3y-1=0.
点评 本题考查了由两点坐标求直线斜率以及两条直线垂直,斜率之积为-1的应用问题,也考查了求直线方程的应用问题,是基础题目.

练习册系列答案
相关题目
5.棱长为2的正方体被一平面截得的几何体的三视图如图所示,那么被截去的几何体的体积是( )


| A. | $\frac{14}{3}$ | B. | $\frac{10}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
12.已知x1、x2是函数f(x)=|lnx|-e-x的两个零点,则x1x2所在区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
8.对椭圆C1;$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和椭圆C2;$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的几何性质的表述正确的是( )
| A. | 范围相同 | B. | 顶点坐标相同 | C. | 焦点坐标相同 | D. | 离心率相同 |
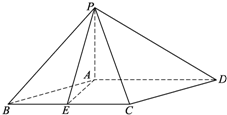 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.