题目内容
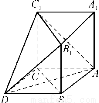
在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为线段BC的中点,E、F为线段AC的三等分点(如图①).将△ABD沿着AD折起到△AB′D的位置,连结B′C(如图②).
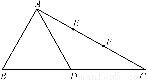
图①

图②
(1)若平面AB′D⊥平面ADC,求三棱锥B′-ADC的体积;
(2)记线段B′C的中点为H,平面B′ED与平面HFD的交线为l,求证:HF∥l;
(3)求证:AD⊥B′E.
(1) (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】(1)解:在直角△ABC中,D为BC的中点,所以AD=BD=CD.又∠B=60°,所以△ABD是等边三角形.取AD中点O,连结B′O,所以B′O⊥AD.因为平面AB′D⊥平面ADC,平面AB′D∩平面ADC=AD,B′O?平面AB′D,所以B′O⊥平面ADC.在△ABC中,∠BAC=90°,∠B=60°,AB=1,D为BC的中点,所以AC=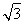 ,B′O=
,B′O=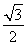 .所以S△ADC=
.所以S△ADC=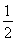 ×
× ×1×
×1×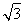 =
=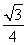 .所以三棱锥B′ADC的体积为V=
.所以三棱锥B′ADC的体积为V=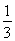 ×S△ADC×B′O=
×S△ADC×B′O= .
.
(2)证明:因为H为B′C的中点,F为CE的中点,所以HF∥B′E.又HF?平面B′ED,B′E?平面B′ED,所以HF∥平面B′ED.因为HF 平面HFD,平面B′ED∩平面HFD=l,所以HF∥l.
平面HFD,平面B′ED∩平面HFD=l,所以HF∥l.
(3)证明:连结EO,由(1)知,B′O⊥AD.
因为AE=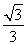 ,AO=
,AO=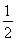 ,∠DAC=30°,
,∠DAC=30°,
所以EO=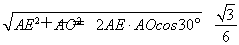 .
.
所以AO2+EO2=AE2.所以AD⊥EO.
又B′O 平面B′EO,EO
平面B′EO,EO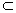 平面B′EO,B′O∩EO=O,
平面B′EO,B′O∩EO=O,
所以AD⊥平面B′EO.
又B′E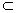 平面B′EO,所以AD⊥B′E.
平面B′EO,所以AD⊥B′E.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目