题目内容
【题目】（本小题满分13分）设数列
的前
项和为
.已知
， 
， 
.
（1）写出
的值，并求数列
的通项公式；
（2）记
为数列
的前
项和，求
；
（3）若数列
满足
， 
，求数列
的通项公式.
【答案】（1）
；（2）
；（3）
。
【解析】试题分析：（Ⅰ）由已知得， 
， 
. …………………2分
由题意， 
，则当
时， 
.
两式相减，得
（
）. ………………………3分
又因为
， 
， 
，
所以数列
是以首项为
，公比为
的等比数列，
所以数列
的通项公式是
（
）. ………………………………4分
（Ⅱ）因为
，
所以
， ……………………5分
两式相减得， 
， ………7分
整理得， 
(
). ………………………………8分
（Ⅲ） 当
时，依题意得
,
,… , 
.
相加得， 
. …………………11分
依题意
.
因为
，所以
（
）.
显然当
时，符合.
所以
(
). …………………13分
【题目】设某地区乡居民人民币储蓄存款（年底余额）如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
（1）求关于
的回归方程
，并预测该地区2019年的人民币储蓄存款（用最简分数作答）.
（2）在含有一个解释变量的线性模型中，
恰好等于相关系数
的平方，当
时，认为线性回归模型是有效的，请计算并且评价模型的拟合效果（计算结果精确到
）.
附：
, 
.
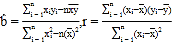【题目】语音交互是人工智能的方向之一，现在市场上流行多种可实现语音交互的智能音箱，它们可以通过语音交互满足人们的部分需求.经市场调查，某种新型智能音箱的广告费支出x（万元）与销售额y（单位：万元）之间有如下对应数据：
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
（1）求y关于x的线性回归方程（数据精确到0.01）；
（2）利用（1）中的回归方程，预测广告费支出10万元时的销售额.
附：回归直线的斜率和截距的最小二乘估计公式分别为：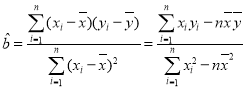
，
.